BESS overview

When distributing the workload over \(n\) workers (=IPUs), BESS randomly splits the entity embedding table into \(n\) shards of equal size, each of which is stored in a worker’s memory. The embedding table for relation types, on the other hand, is replicated across workers, as it is usually much smaller.

Figure 1. Entity table sharding across \(n=3\) workers.

The entity sharding induces a partitioning of the triples in the dataset, according to the shard-pair of the head entity and the tail entity. At execution time (for both training and inference), batches are constructed by sampling triples uniformly from each of the \(n^2\) shard-pairs. Negative entities, used to corrupt the head or tail of a triple in order to construct negative samples, are also sampled in a balanced way to ensure a variety that is beneficial to the final embedding quality.

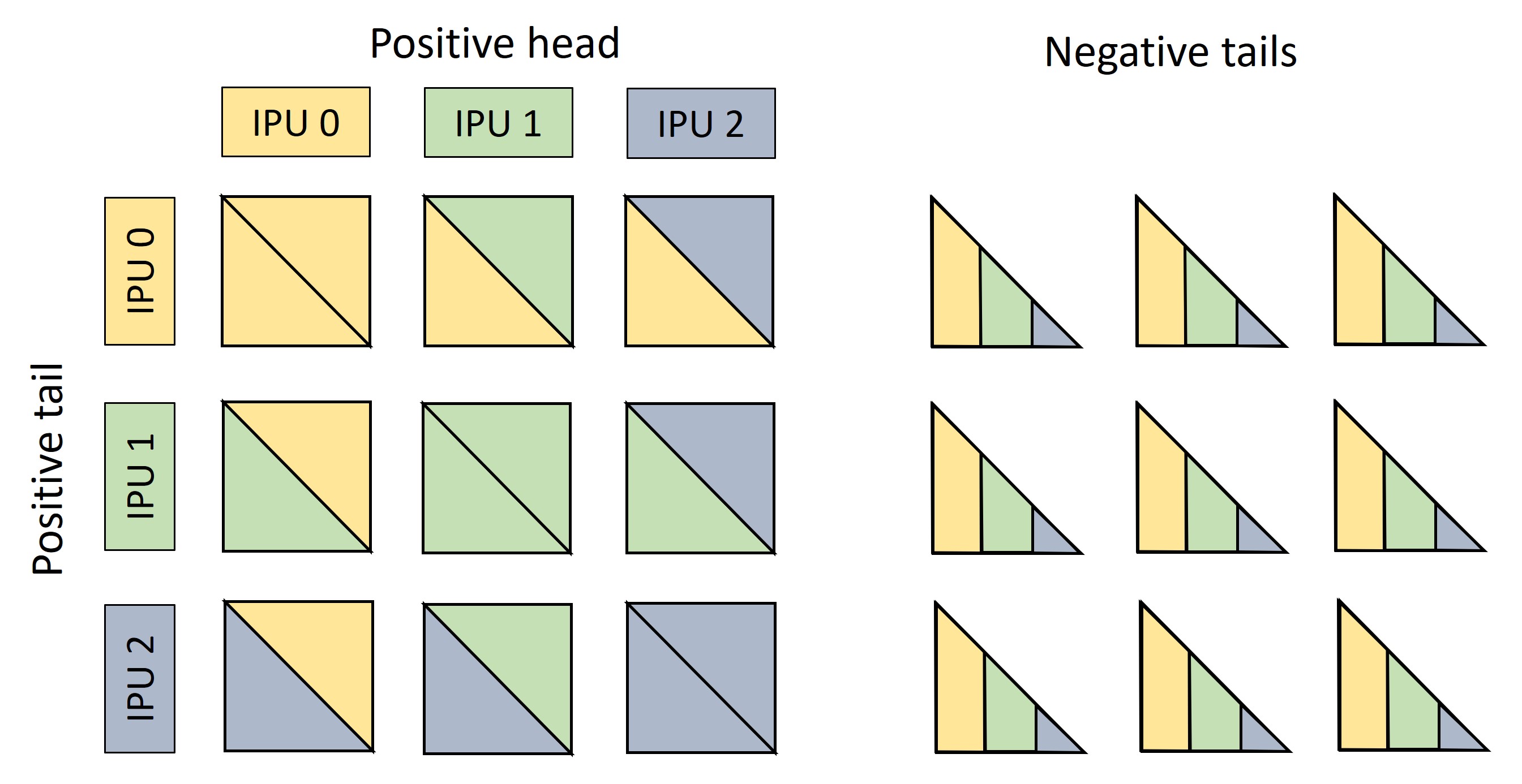
Figure 2. Left: A batch is made up of \(n^2=9\) blocks, each containing the same number of triples. The head embeddings of triples in block \((i,j)\) are stored on worker \(i\), the tail embeddings on worker \(j\), for \(i,j = 0,1,2\). Right: the negative entities used to corrupt triples in block \((i,j)\) are sampled in equal numbers from all of the \(n\) shards (possibly with padding at inference time). In this example, negative samples are constructed by corrupting tails.

This batching scheme allows us to balance workload and communication across workers. First, each worker needs to gather the same number of embeddings from its on-chip memory, both for positive and negative samples. These include the embeddings needed by the worker itself, and the embeddings needed by its peers.

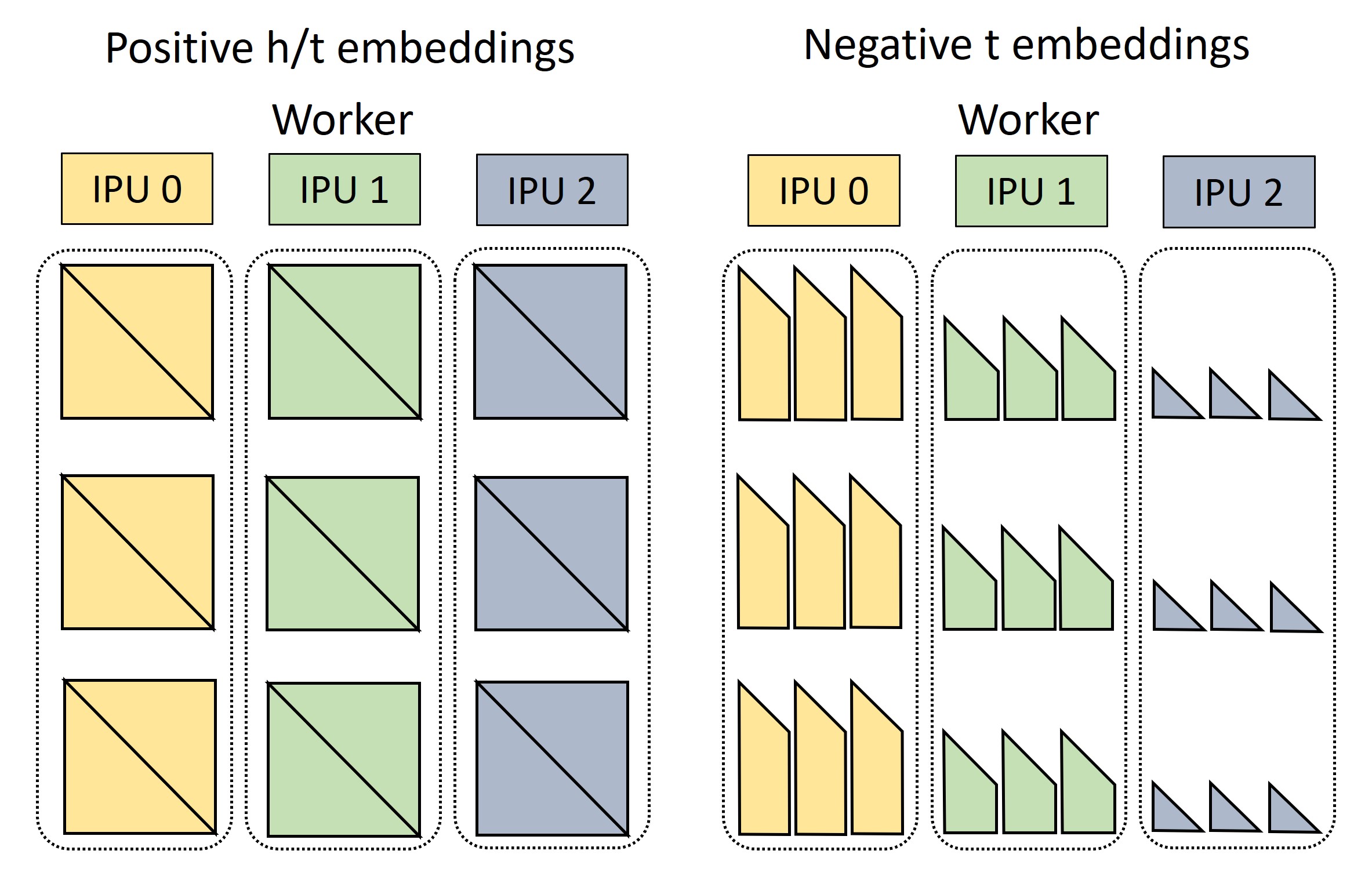
Figure 3. The required embeddings are gathered from the IPU SRAM. Each worker needs to retrieve the head embeddings for \(n\) positive triple blocks, and the same for tail embeddings (the \(3 + 3\) triangles of same colour in Figure 2 (left)). In addition to that, the worker gathers the portion (=\(1/n\)) stored in its memory of the negative tails needed by all of the \(n^2\) blocks.

The batch in Figure 2 can then be reconstructed by sharing the embeddings of positive tails and negative entities between workers through a balanced AllToAll collective operator. Head embeddings remain in place, as each triple block is then scored on the worker where the head embedding is stored.

Figure 4. Embeddings of positive and negative tails are exchanged between workers with an AllToAll collective (red arrows), which effectively transposes rows and columns of the \(n^2\) blocks in the picture. After this exchange, each worker has the embeddings of the correct \(n\) blocks of positive triples and \(n\) blocks of negative tails to compute positive and negative scores.

The distribution scheme presented above is implemented in besskge.bess.EmbeddingMovingBessKGE. While communication is always balanced, exchanging negative embeddings between workers can turn out to be expensive when using many negative samples per triple, or when the embedding dimension is large. In these cases, using besskge.bess.ScoreMovingBessKGE can increase overall throughput. This alternative distribution scheme works in the same way as besskge.bess.EmbeddingMovingBessKGE for the sharding of entities and partitioning of triples, as well as for the way embeddings for positive triples are shared through AllToAll collectives and scored. The difference lies in how negative scores are computed: instead of sending negative embeddings to the query’s worker, all queries are replicated on each device through an AllGather collective, scored against the (partial) set of negatives stored on the device and then the scores are sent to the correct worker via a new, balanced AllToAll. This allows us to communicate negative scores instead of negative embeddings, which is cheaper, although it requires additional collective communications between devices.

Figure 5. Through an AllGather collective, the head embeddings of the \(n^2\) blocks are replicated on all workers. These are then scored against the corresponding negative tails stored on the worker.

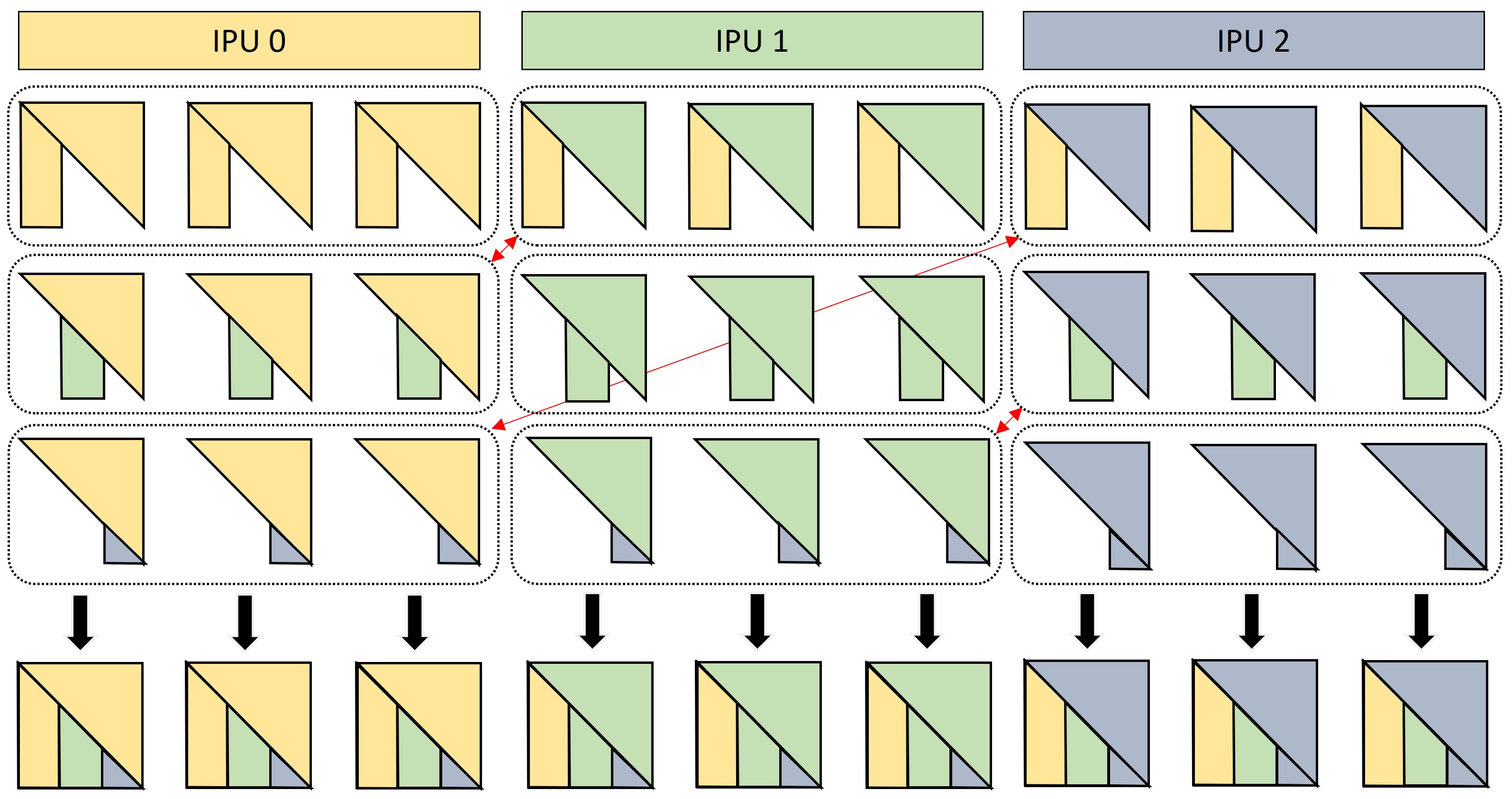
Figure 6. Using a final AllToAll (red arrows) the partial negative scores are put back on the worker where the head embeddings came from. After this, each worker has the complete set of negative scores for each of the \(n\) triple blocks it is responsible for.