Contextual Position Encoding: Learning to Count What’s Important

The key idea

Transformers rely on Position Encoding (PE) to inject information about the position of tokens in a sequence into the attention block, which by construction is order-invariant. This paper proposes Contextual Position Encoding (CoPE), a flexible, context-dependent technique for measuring positional distances at higher abstraction levels than just counting tokens, improving performance on language modelling and addressing common failures of LLMs in counting-based tasks.

Background

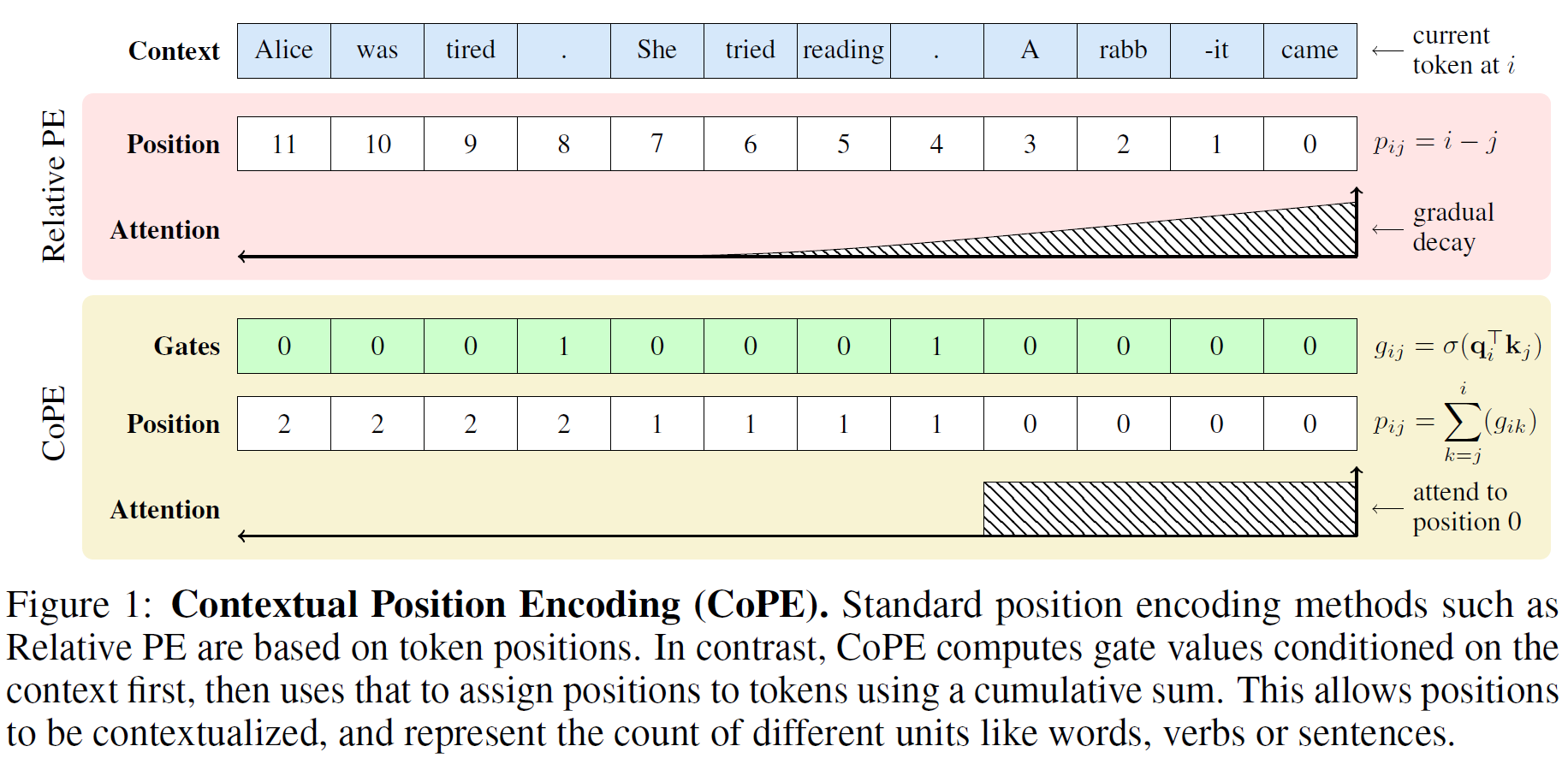
PE introduces learnable position embeddings $\mathbf{e}_{i,j}$ into the attention block

$$ \mathbf{o}_i = \sum_{j < i} \textrm{Softmax}(\mathbf{q}_i^T (\mathbf{k}_j + \mathbf{e}_{i,j})) \mathbf{v}_j$$

with $\mathbf{e}_{i,j} = \mathbf{e}[i]$ for Absolute PE, or $\mathbf{e}_{i,j} = \mathbf{e}[i - j]$ in the case of Relative PE. A clear limitation of this setup is that positions are always measured in terms of tokens, which - depending on the task - might not be the best unit of measure. For instance, state-of-the-art LLMs (like GPT4) are observed to often fail at simple counting tasks that require them to attend only to tokens or words within specific chunks of text, like sentences or paragraphs, that can have highly variable lengths.

Their method

In CoPE, the distance of token $j$ with respect to the query position $i$ (with $j < i$) is measured based on the context of the intermediate tokens, through a soft gate:

$$p_{i,j} = \sum_{t=j}^i g_{i,t}, \; \text{ with}\; g_{i,t}=\sigma(\mathbf{q}_i^T \mathbf{k}_t) \in (0,1).$$

In the attention computation we then use $\mathbf{e}_{i,j} = \mathbf{e}[p_{i,j}]$ or, in the case where $p_{i,j}$ is not an integer, an interpolation of $\mathbf{e}[\lfloor p_{i,j} \rfloor]$ and $\mathbf{e}[\lceil p_{i,j} \rceil]$.

Relative PE can be seen as the limit case where all $g_{i,t} = 1$. More generally though, thanks to context-awareness, $p_{i,j}$ could be the count of a specific word, or the number of sentences, between token positions $j$ and $i$, or any other measure that the model finds useful to track. Note that, by construction, each attention head and each layer will compute a different $p_{i,j}$, thus allowing the model to represent different levels of position abstraction at the same time.

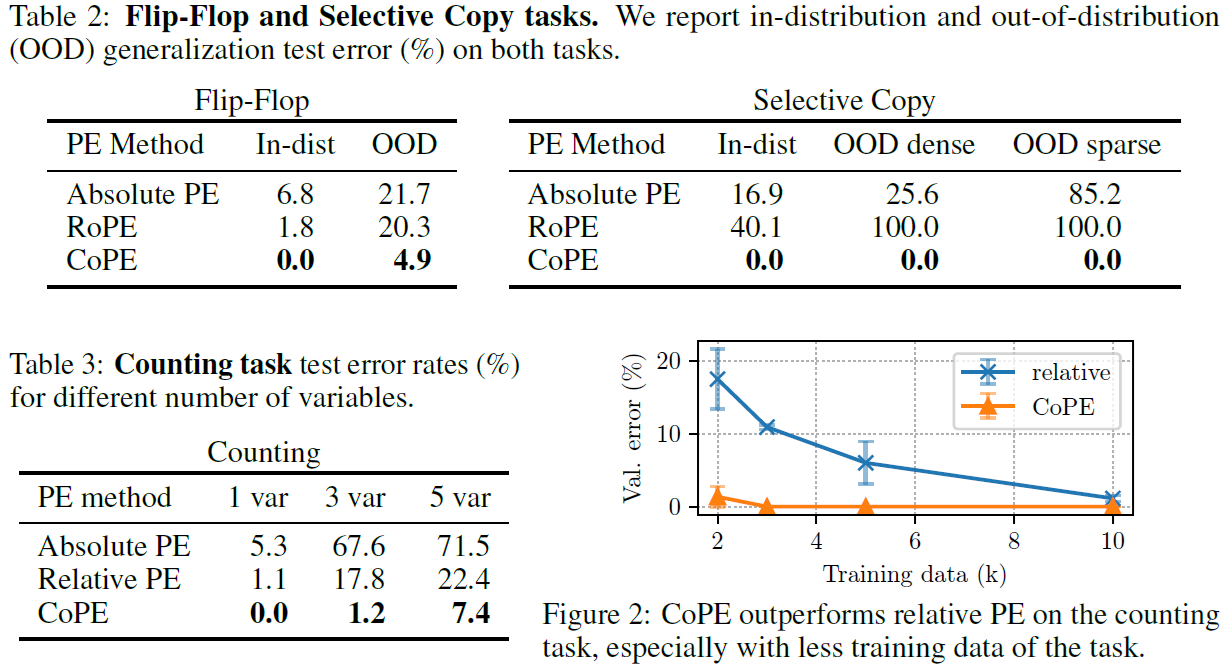
Results

CoPE is tested on a variety of artificial tasks (like selective copying/counting and the Flip-Flop task) where standard PE methods perform poorly. For all of them, CoPE yields strong improvements and better generalisation to out-of-distribution data.

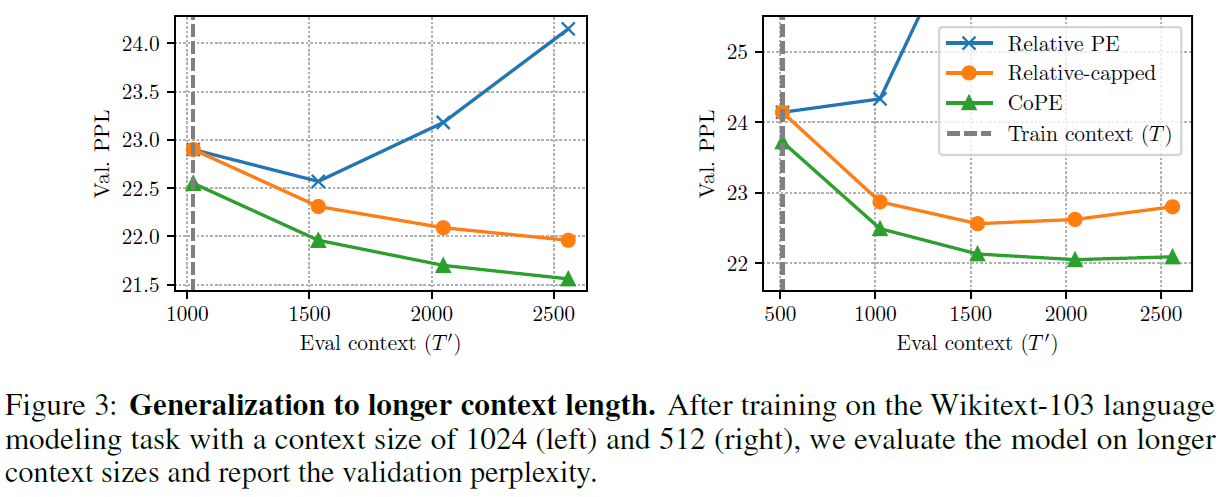
Moreover, CoPE improves in perplexity over Relative PE for language and code modelling with small Transformers (20M-100M parameters), also showing better generalisation to longer contexts than the ones seen in training.

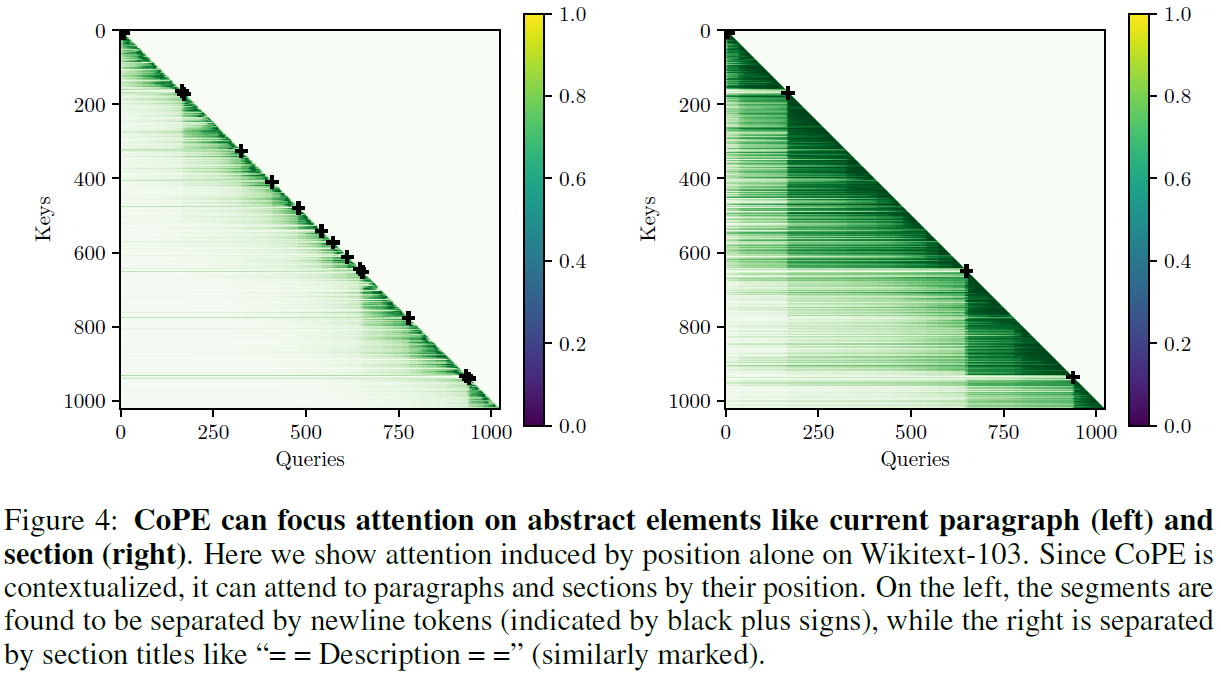
Takeaways

Despite the limited scale of experiments, the results show a promising step in the direction of making the reasoning and abstraction abilities of Transformers even more flexible. It will be interesting to see how CoPE performs on larger models, and quantify the trade-off between performance gains and additional computation costs on real-world downstream tasks.