Scaling FP8 training to trillion-token LLMs

The key idea

Building upon recent literature on low-precision FP8 training, the authors investigate the FP8 training stability of trillion-token LLMs (a ~20-fold increase over previous published work). Uncovering a new form of critical instability, they present an improved Smooth-SwiGLU activation function which prevents activation spikes (outliers) from causing training divergence in LLMs.

Training instability in FP8 due to the SwiGLU activation function.

Background

Machine learning researchers, especially in AI hardware companies, have been investigating for the last couple of years which 8-bit floating formats are suitable for neural network training and inference. The literature on the subject converges towards the definition of two formats: E4M3 and E5M2. The former is used to represent weights and activations, while the latter is used for gradients, which require a higher dynamic range.

Due to the much smaller dynamic range compared to BF16 (which is commonly used in LLM training), FP8 LLM training requires ad-hoc per tensor scaling using data statistics (usually the absolute-max) in order to keep training stable.

Most of the FP8 literature has focused on small to mid-scale experiments (at most 100B tokens training), and presented in this work, late-stage LLMs training also presents numerical stability challenges, with large outliers appearing in the transformer feed-forward layer.

Their method

As presented in the figure above, instabilities appear in late FP8 training of large LLMs. In this work, the authors narrow down the issue to the quadratic form of the SwiGLU activation function when combined with weight alignment. Experimental training data shows that large outliers appear more often during late training due to the correlation between w1 and w2 SwiGLU weights (which are uncorrelated initially).

SwiGLU weights correlation and outliers.

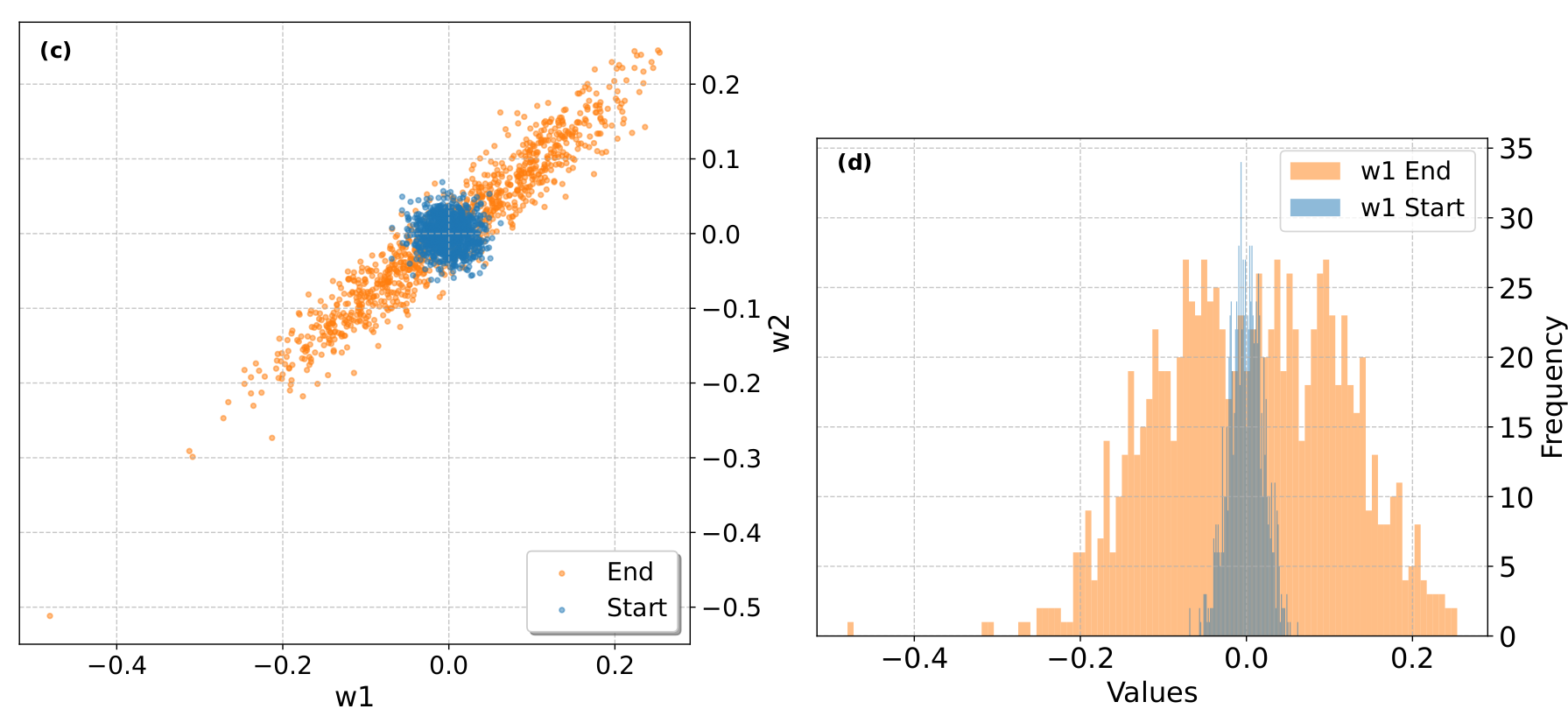
These outliers will lead to underflow or overflow during FP8 quantization when combined with delayed scaling, as the latter technique relies on the previous batch statistics for optimal hardware usage. In order to circumvent this issue, the authors introduce a new smooth SwiGLU activation function which incorporates channel scaling correction prior to FP8 casting, i.e.:

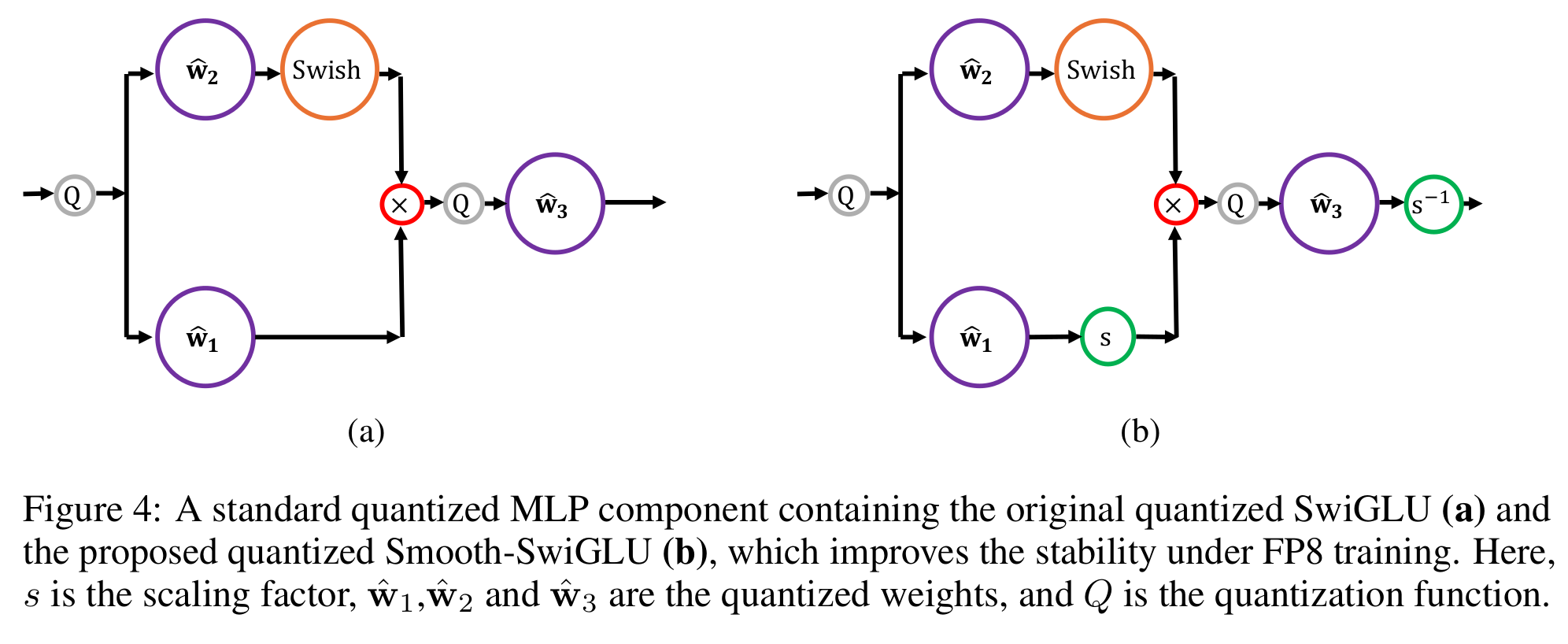
As presented by the authors, channel max-scaling is well suited to hardware accelerator as each chunk of data can be treated in parallel, and the resulting rescaling can be fused into the FP8 quantization of input activations $x$ and weights $w_3$ (third MLP layer):

Smooth-SwiGLU definition.

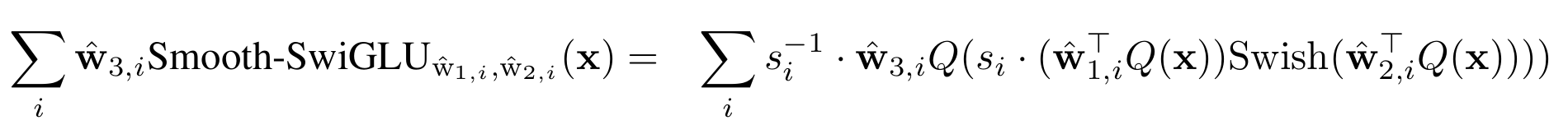
We note that the introduction of the smooth-SwiGLU activation preserves the overall FFN definition (from a mathematical point of view): additional channel scaling factors are compensated later in the network in the third MLP layer. We at Graphcore Research have proposed a similar approach in our recent Scalify work: incorporating additional scaling in neural networks to improve numerical stability while keeping the same model definition.

Results

Training experiments on a 7B Llama 2 model show the improved stability of FP8 LLM training when using the smooth-SwiGLU activation: training loss as well as zero-shot downstream tasks match the BF16 baseline. The use of smooth-SwiGLU only leads to a small drop in FP8 training acceleration, from 37% to 34%, due to the cost of channel rescaling.

FP8 LLM training with Smooth-SwiGLU.

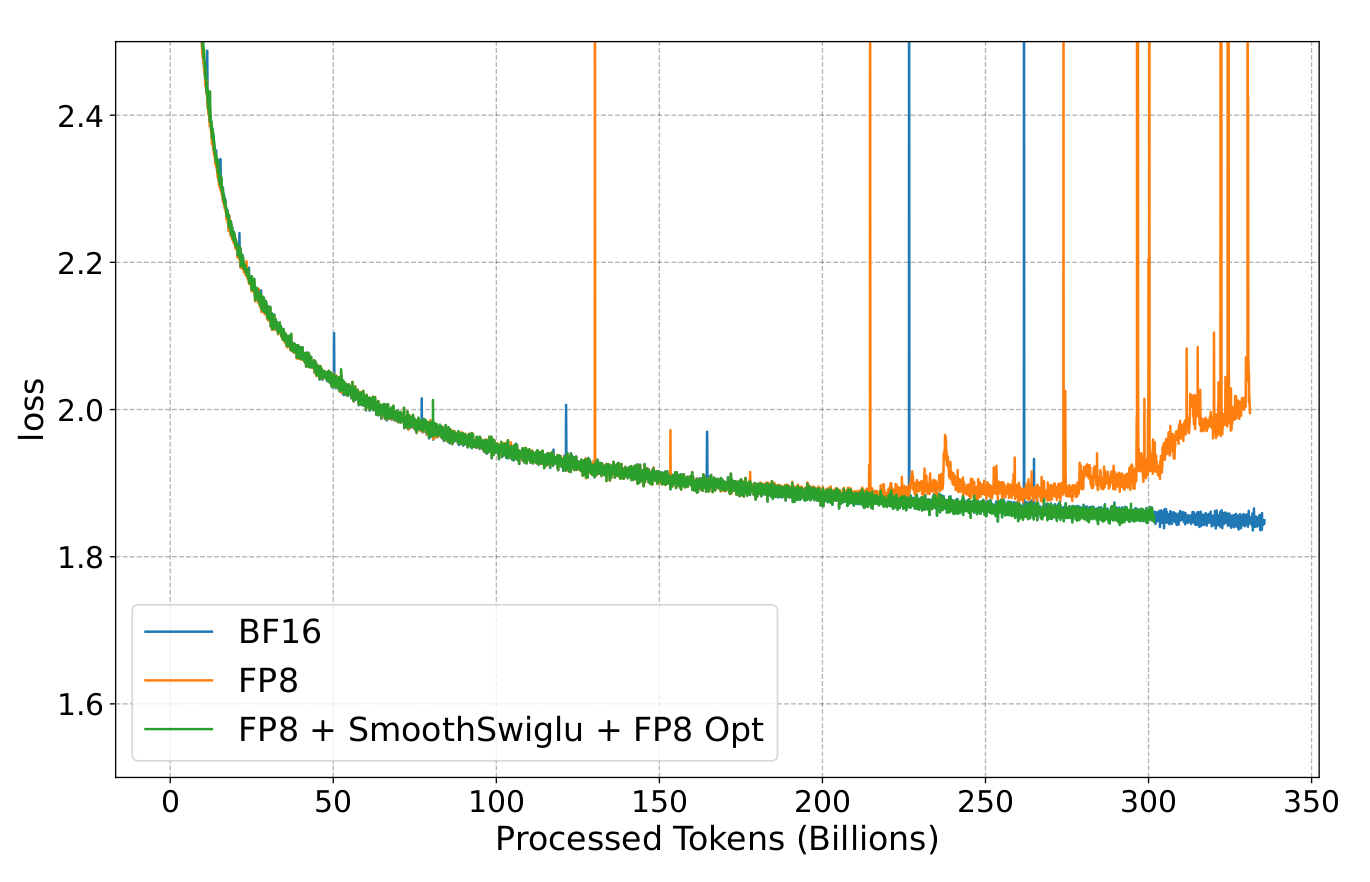
The authors also demonstrate that the FP8 E5M2 format can be used for storing the Adam optimizer second moment (as presented in previous works, the first moment can be represented using E4M3).