GaLore: Memory-Efficient LLM Training by Gradient Low-Rank Projection

The key idea

Training and fine-tuning Large Language Models (LLMs) on consumer accelerated hardware has been a challenge due to significant memory requirements as model size increased. As a consequence, a large literature has emerged around low-rank approximation of model weights, including the well-known LoRA method. This work proposes a low-rank approximation of gradients instead of weights, leading to similar memory savings while improving accuracy in pre-training applications.

Background

The well-known Low-Rank Adaptation (LoRA) method reparameterizes a weight matrix $W$ by using a low-rank projection:

$$ W = W_0 + BA $$

where $W_0\in R^{m \times n}$ are (usually) frozen pre-training weights, $A\in R^{m \times r}$ and $B\in R^{r \times n}$ are trainable low-rank adaptors. Since $r$ is chosen much smaller than $m$ and $n$, the use of LoRA reduces massively memory usage, opening the door to fine-tuning of LLMs on consumer hardware.

Their method

The authors of GaLore propose to apply low-rank approximation to the gradients instead of weights, reducing memory usage similarly to LoRA as well as opening the door to pretraining on consumer hardware. The authors prove that the gradients become low-rank during training, with a slowly evolving projection subspace.

In this algorithm, the model is left unchanged, but the training loop is modified as following:

for weight in model.parameters():
    grad = weight.grad
    # original space -> compact space
    lor_grad = project(grad)
    # update by Adam, Adafactor, etc.
    lor_update = update(lor_grad)
    # compact space -> original space
    update = project_back(lor_update)
    weight.data += update

where project and project_back are defined as:

$$ \text{project}(G_t) = P_t^T G_t Q_t \quad\text{and}\quad \text{project_back}(\tilde{G_t}) = P_t G_t Q_t^T $$

Similarly to LoRA, the projection space rank $r$ is chosen much smaller than $m$ and $n$, leading to reduced memory usage on gradients and optimizer state. Matrices $P_t$ and $Q_t$ are estimated via a Singular Value Decomposition (SVD) on the full rank gradient $G_t$, and are updated every ~50-1000 training iterations (accuracy being fairly stable within this interval).

Results

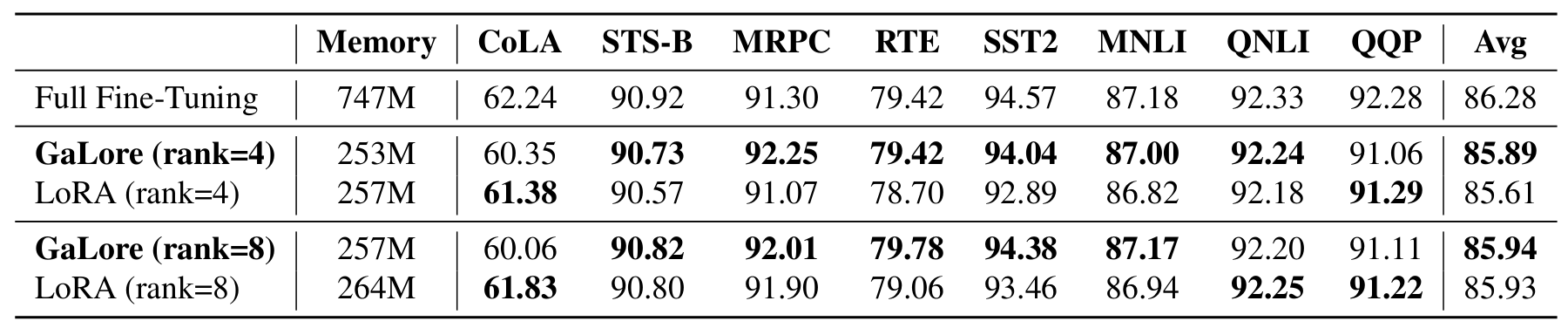
On fine-tuning tasks, GaLore and LoRA achieve close accuracy and memory consumption.

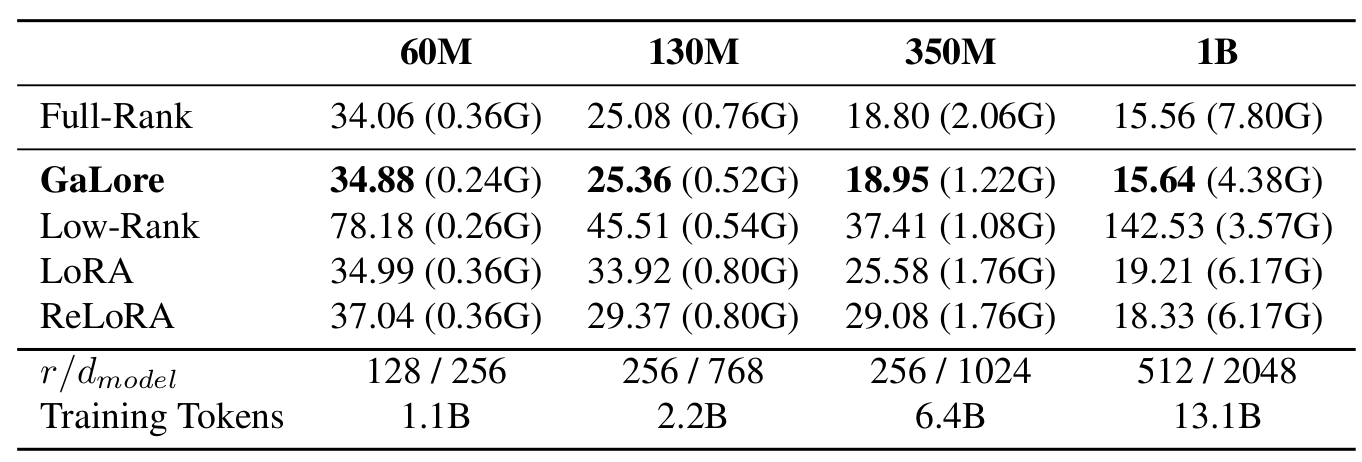
Additionally, GaLore shows much better performance on LLaMA pretraining compared to LoRA and ReLoRA, while using significantly less memory. Interestingly, for pre-training, the subspace rank $r$ can be seen as an hyperparameter trading-off memory and compute budgets (i.e. a smaller rank requires more iterations to achieve similar accuracy).

Takeaways

GaLore offers a compelling and accurate alternative to LoRA for memory efficient LLM pre-training and fine-tuning, with the main advantage of being an off-the-shelf pure optimizer algorithm. As mentioned by the authors, an interesting extension of this work would be to investigate how to integrate quantization, in the vein of QLoRA, to push further model size on customer hardware.