Metacognitive Reuse: Turning Recurring LLM Reasoning Into Concise Behaviors
The key idea
“Do not rediscover the wheel, if you have already done it once!”
– paraphrased TL;DR
According to Didolkar et al., this is the key lesson we should teach LLMs. Why? The authors have observed that while rapid progress in the performance of Chain-of-Thought approaches has been made, this has also led to an effectiveness/efficiency decline. From where? Because the LLMs re-derive knowledge from scratch too often, resulting in less room for exploration and larger token output.
The proposed remedy is metacognitive reuse. Instead of providing a set of facts/rules, we let the LLMs synthesise their own behaviours. These are concise pieces of knowledge, reusable across questions/datasets and models.
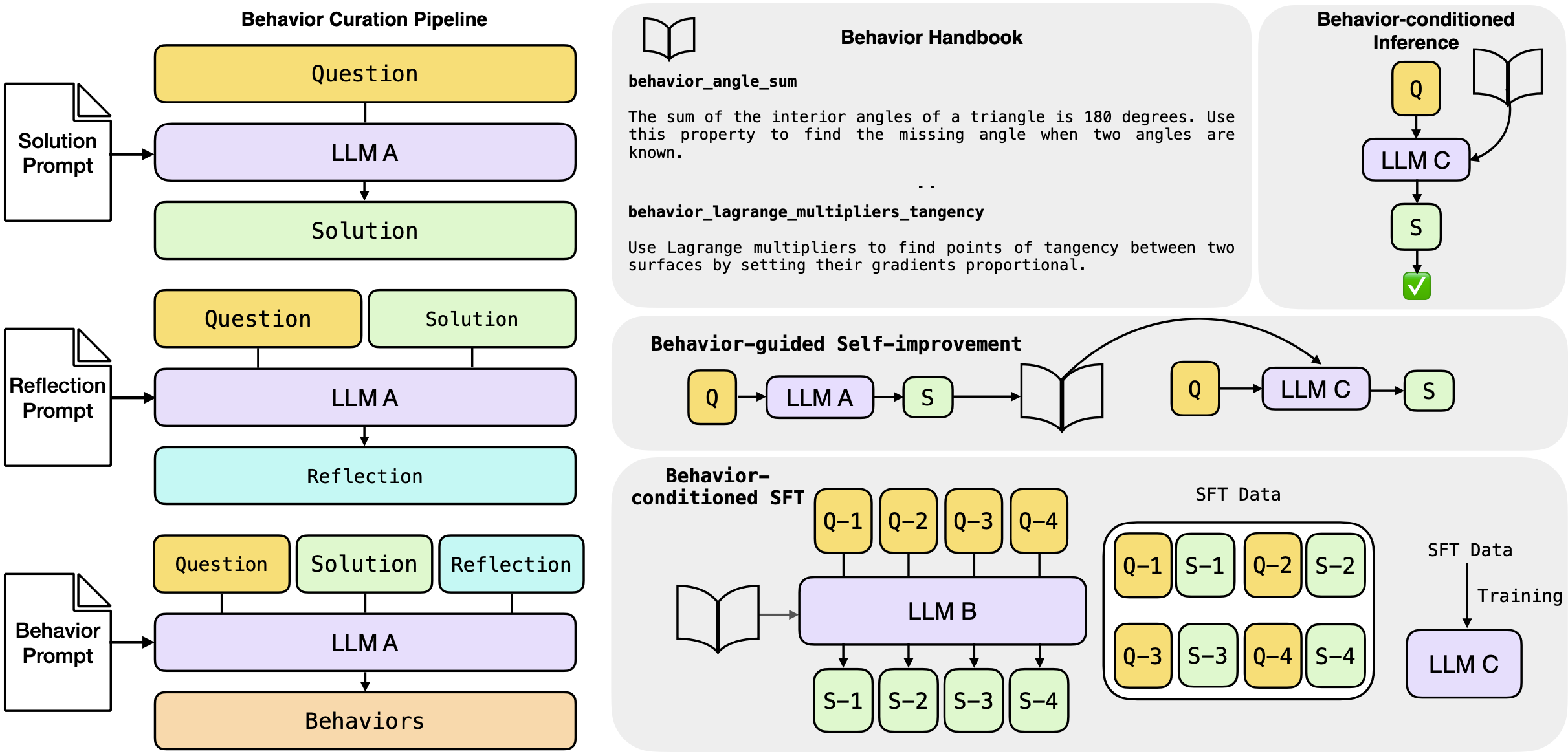
Behaviour Curation Pipeline (left): All the 3 stages of behaviour curation pipeline: solution, reflection, extraction. LLM A is referred to as the Metacognitive Strategist. Reasoning with behaviours (right; in gray): The three proposed ways to utilise behaviours – inference, self-improvement and supervised fine-tuning (SFT). LLM B and LLM C are a student and teacher LLMs respectively.
Once synthesised, Didolkar et al. propose three ways to utilise extracted behaviours:
- Behaviour-conditioned inference (BCI) – the set of behaviours is pre-extracted from a (different) strategist LLM.
- Behaviour-guided self-improvement – the set of behaviours is extracted as we process questions/tasks from the same LLM.
- Behaviour-conditioned supervised fine-tuning – a Behaviour-conditioned teacher model synthesises a training set of question/solution pairs, used to fine tune the student model.
Background
Chain-of-Thought (CoT) prompting is a technique in prompt engineering for large language models. It encourages the LLM to break down complex reasoning tasks into a sequence of intermediate reasoning steps (a “chain”) before arriving at a final answer. This helps improve performance on multi-step problems (e.g. arithmetic, logic, commonsense) at the cost of outputting long reasoning traces (more output tokens = higher expenditure). Unfortunately, the chain might still be flawed. More enumerative beam-search-like approaches, can resolve this, but the computation required is even higher.
Their method
Behaviour curation There is a lack of formal definition of behaviour. At the risk of repeating myself, authors define it in the main text as “a reusable skill—concise piece of knowledge—distilled from an LLM’s chain of thought” (p.4). E.g.:
behaviors_angle_sum: The sum of the interior angles of a triangle is 180 degrees. Use
this property to find the missing angle when two angles are known.
The proposed extraction pipeline consists of three stages. The Metacognitive Strategist (DeepSeek-R1-Distill-Llama-70B) first generates a reasoning trace + a final answer. These are then used for the reflection prompt, which is also fed back to the same LLM, to allow it to filter out illogical chains and also generate new candidate behaviours. The Metacognitive Strategist is also used for the generation of the final set of behaviours, which are to be appended to the behaviour handbook.
Out of the three prompts, perhaps the most insightful is the reflection prompt. Behaviour is defined there as “a note or skill”, which “can be a strategy, a trick, or a technique”, or “it can also be a general rule or a commonsense principle”, and, most importantly, “is not a solution to the problem, but can be used to solve it”. Correctness analysis prompting aside, the authors explicitly require the model to consider how a behaviour “would have helped in reducing the answer length”.
Behaviour usage$\approx$RAG A naive approach to behaviour conditioned inference (BCI) would be to simply make them part of the context. Such an approach, however, would bloat the number of input tokens and, as a result, have higher cost than CoT. The authors also note this: instead of feeding in all behaviours, for a question $Q_i$, a subset of behaviours $B_i$ is retrieved and the solution $S_i$ is generated based on the $(B_i, Q_i)$ pair. The retrieval function depends on the dataset – topic-matching is used for MATH, FAISS top-40 cosine similarity lookup for AIME.
When it comes to Behaviour-guided self-improvement, there is some confusion going on inside me. $\S4.2$ states:
behaviours […] are then fed back […] to solve the same question or new questions
and that the implementation “closely follows that of BCI”. In the experimental setup ($\S5.2$), the text suggests that the approach is a behaviour-guided variant of the Critique-and-Revise baseline and that
[…] reasoning traces are generated per question which are used […] to curate a behaviour handbook for that question
The inline equation $((B, Q),\rightarrow R_2)$ (note the lack of subindexes) also suggest that there is no RAG-like lookup as in BCI, nor that the previously curated behaviours are used for the current or future questions. Whether this is indeed the case or is just a clarity issue with the writeup, only the authors can tell. (Open-sourcing the code to reproduce the experiments could also have answered my questions).
As both of the above approaches use extra input tokens, the authors also present Behaviour-conditioned SFT (BC-SFT). The aim of BC-SFT is to “internalise” the set of behaviours in the weights of the model – when answering any new questions, the fine-tuned model will not be conditioned on a behaviour handbook. It will be invoking those behaviours, based on its parameter weights. Importantly, to achieve that the student model is never conditioned on a handbook, neither during training, nor during inference.
Results
The authors experiment on MATH as well as both AIME (2024, 2025) variants. Behaviour usage (conditioning/self-improvement/SFT) is performed on open-source reasoning LLMs – DeepSeek-R1, which in the plots is referred to as R1-Llama-70B and Qwen. The Metacognitive Strategist model is always fixed to DeepSeek. For MATH, behaviours are synthesised from a subsample of it and for AIME – from past iterations (2022, 20223) of the benchmark. In the plots that follow, while no standard deviations are reported (since we measure both accuracy and token usage, stds could look like an ellipse around each point), results are average across 80 seeds – check paper for further technical details. Unless otherwise stated, the x-axis is the average number of tokens produced per solution and the y-axis is average accuracy. The different symbols are the enforced upper limit on number of output tokens.
N.B. #1 Before we proceed to analyse the plots, please be aware the axis limits vary between plots, sometimes quite drastically (cf. SFT plots). I am aware the authors are trying to make a point, but do not vary limits… at least not within one figure… or at least without being explicit about it.
N.B. #2 For the reader’s entertainment, I have tried to be as independent as possible in my analysis, i.e. only copying plots, but not copy-pasting the authors’ text.
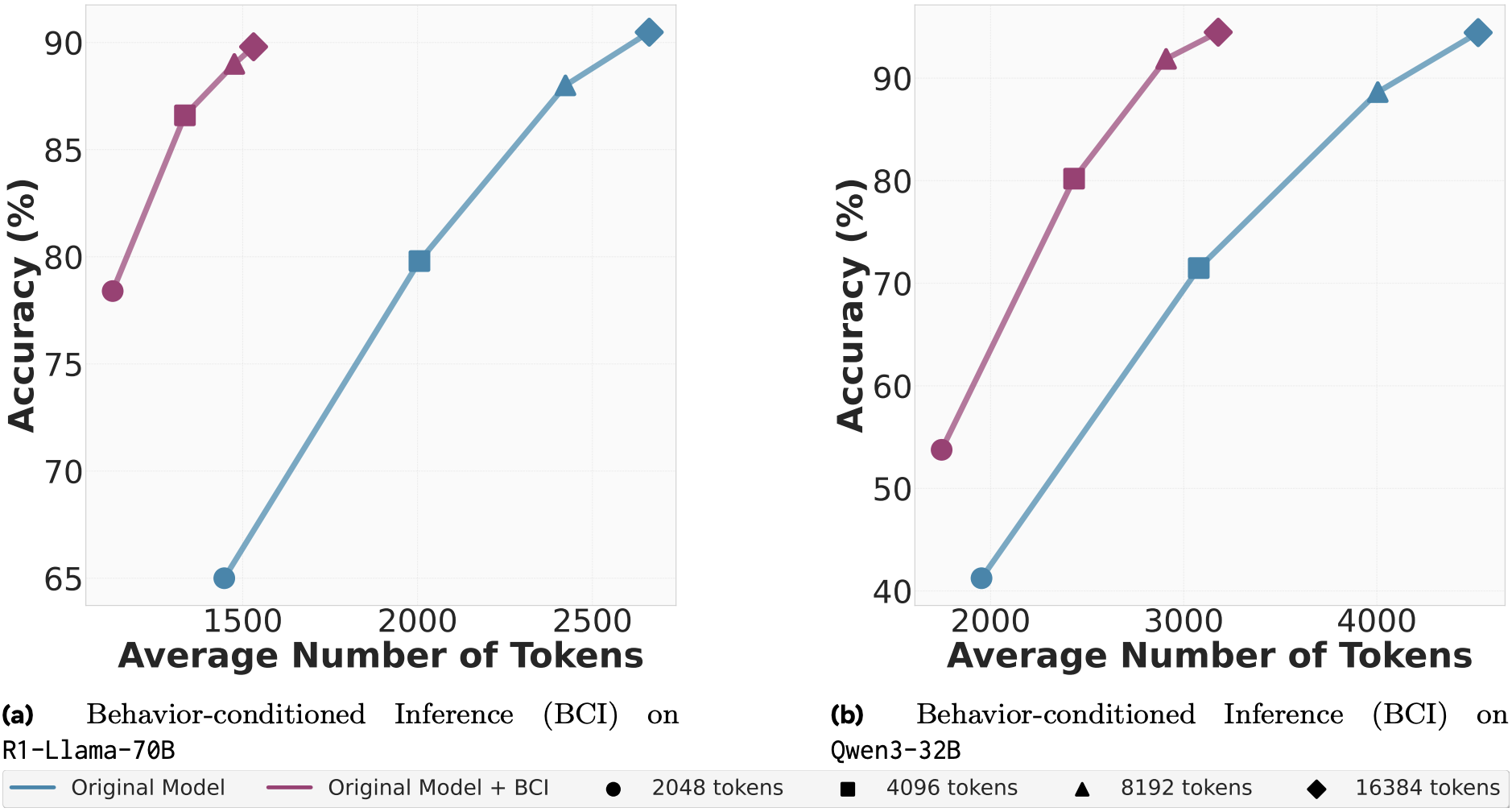
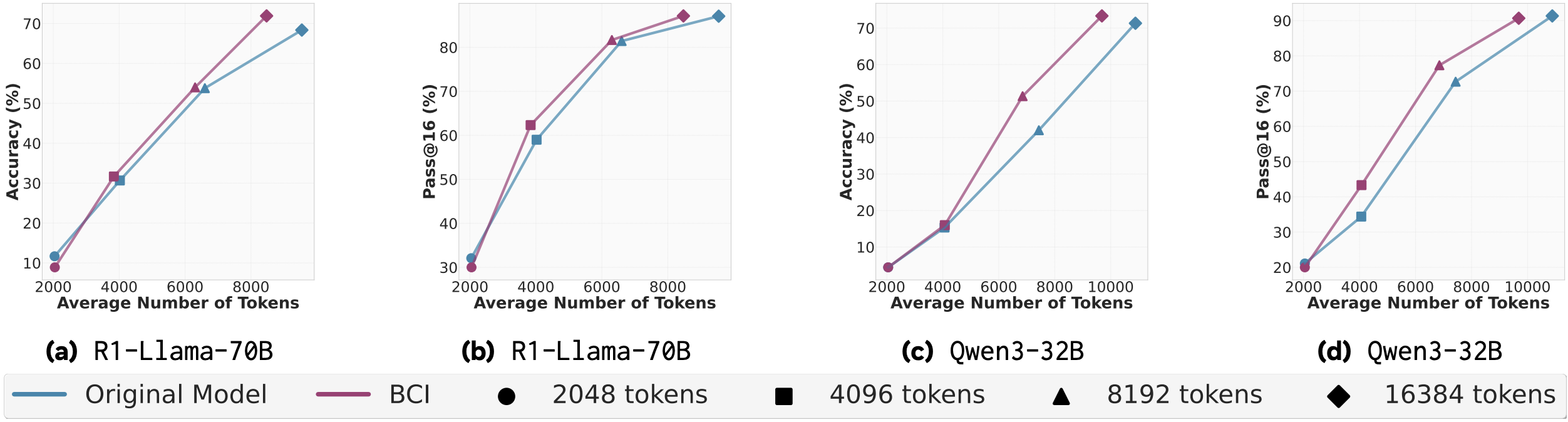
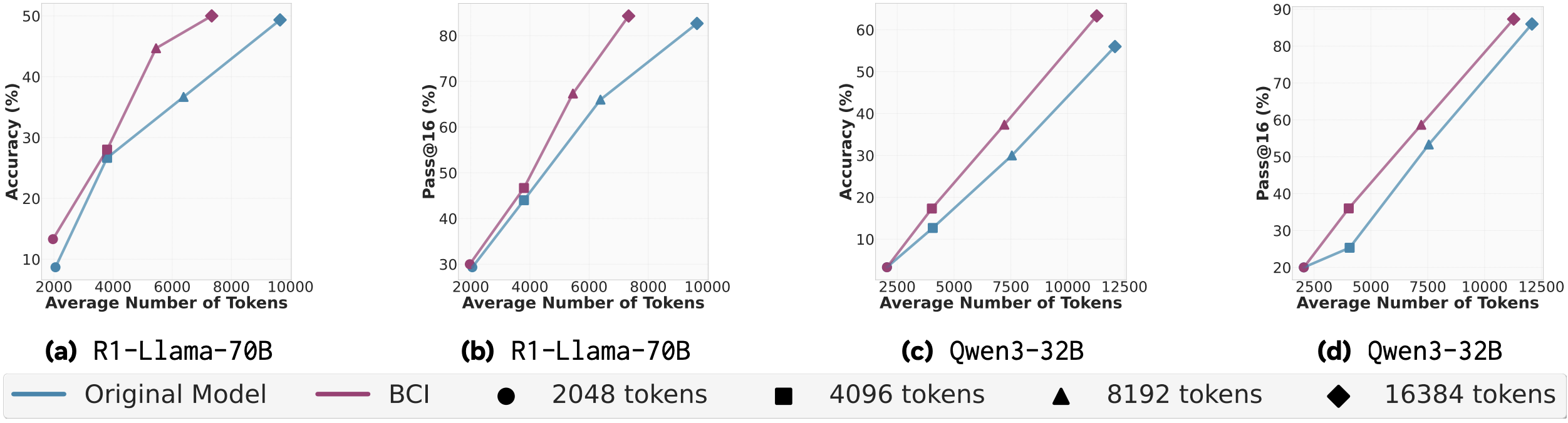
Starting with the BCI performance, there is a clear advantage, both in terms of tokens produced and accuracy on the MATH dataset. This advantage however is much smaller and questionable, without standard deviations, on both AIME variants, especially at lower token limits (2048 and 4096). At higher token limits, we do see more substantial improvements, particularly for BCI with DeepSeek. While concrete numbers would certainly have been appreciated, the reduction in output tokens for DeepSeek seemingly varies between 5% and 30%. Upon visual inspection, such reductions are much rarer for Qwen. In all cases, accuracy is preserved or improved (sometimes slight, sometimes substantial, hard to judge visually).
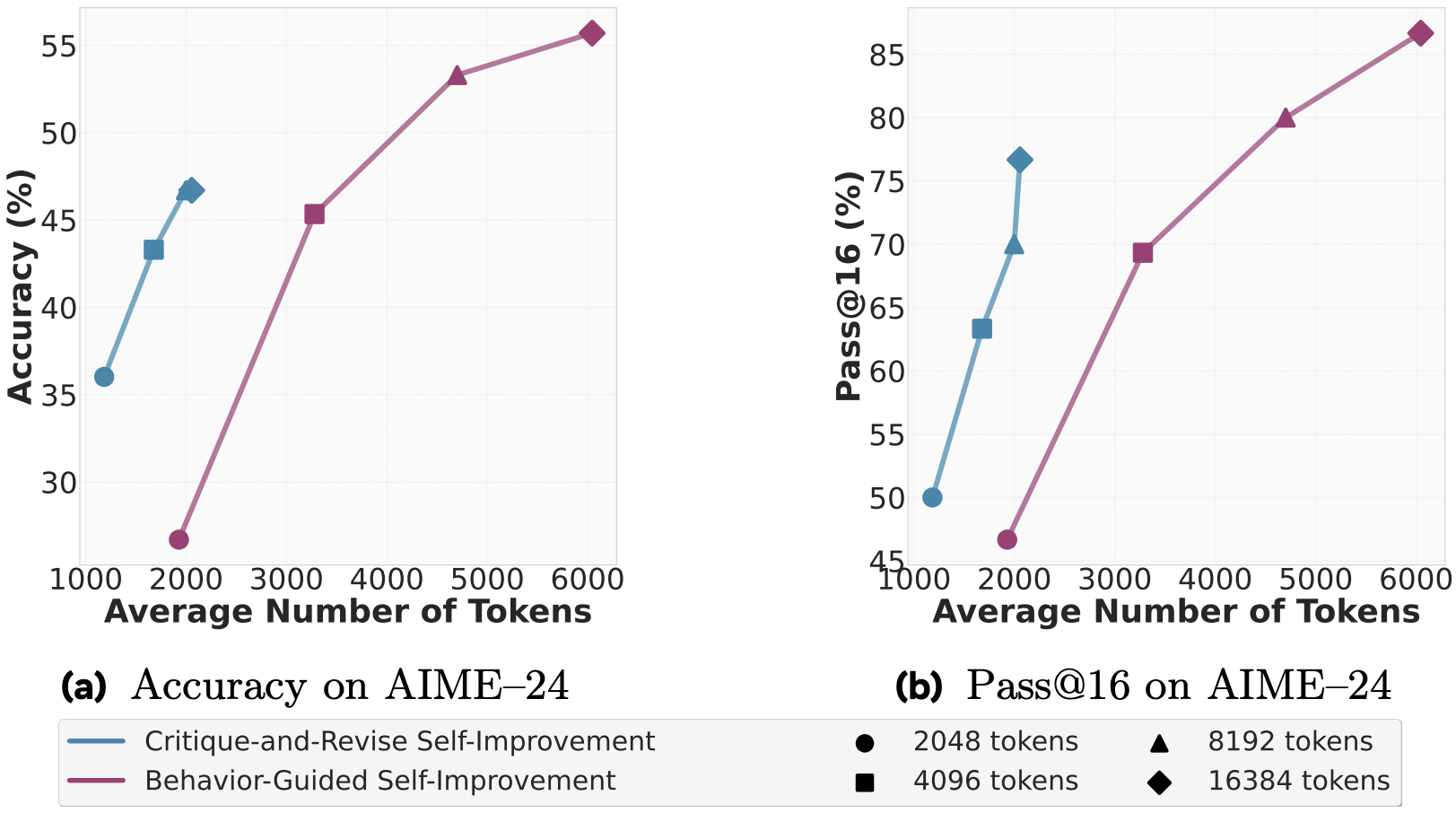
Again, for self-improvement, analysis of results can be split into two parts – for the 2048 token limit, behaviours hurt more than help as there is both an increase in tokens produced and a drop in accuracy. For larger limits, and especially the largest, behaviour-guided self-improvement can give 10% boost in the accuracy and 20% boost in Pass@16., but at the cost of threefold increase in the output tokens. Also note, that for this result, there is the ambiguity if the behaviour handbook is synthesised for each question individually or for the whole dataset.
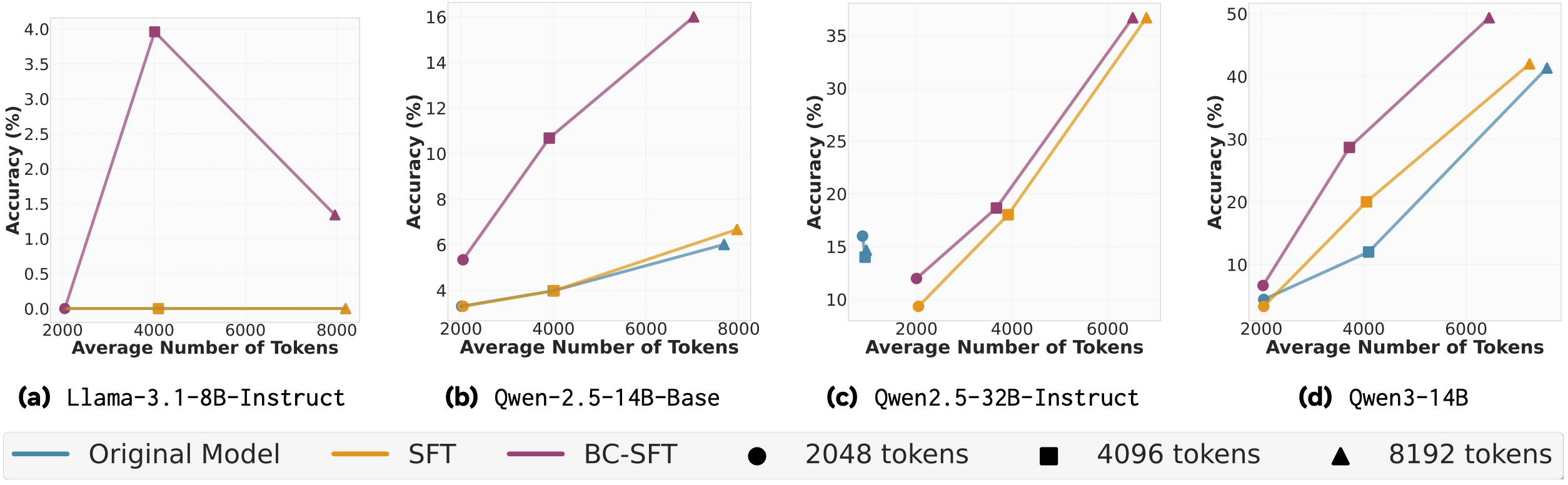
BC-SFT on AIME-24. DeepSeek is the teacher model, each pane is a different student model. Llama-3.1-8B is not DeepSeek!

When it comes to supervised fine tuning, the student model has to have a sufficient capacity in order to grok behaviours – the 8B model’s accuracy is limited to 5%. This conclusion is further reinforced from the fact that BC-SFT results for Qwen-2.5 32B and the lowest token limit often match/exceed accuracy of the 14B variant, across all limits. Newer model variants also benefit more from behaviour conditioning, than past iterations of the same architecture (cf. Qwen3 vs Qwen2.5). And while accuracy improvement to the baseline SFT can be threefold (which is actually 10%, note the scale!) and is observed across all token limits, reduction in the token count is still a larger token limit (8192) luxury. A table with concrete token counts is lacking in the paper, but I would estimate the reduction to be 10-15%.
Takeaways
So, what score would the Reviewer #2 inside me give? Despite my initial hopes, I am leaning towards rejection. The idea of metacognitive-reuse seems novel and exciting enough for me, but the experiments execution is a bit flawed. The authors discuss the efficiency implications of having a larger input but:
- Never state any end-to-end costs – even with amortised computation and cheaper rates on input, this is a necessary information (see below).
- Never visualise how the behaviour handbook grows or analyse its redundancy – out of the 1k subsampled MATH questions, the Metacognitive Strategist extracted 785 behaviours (p. 7). For AIME, out of 16$\times$60=960 reasoning traces – 1457 behaviours (p. 7). On average, the model finds a new pattern from almost every given question! In that case, in a real world scenario, will we need to run the Strategist for every question (requires 3 prompts; cache hits unlikely)?
- Never compare to other, non-prompting, test-time compute scaling techniques, such as latent reasoning – if latent reasoning is both cheaper/more accurate, then the above approach is obsolete. I am not certain that this will be the case, but I call for a comparison.




Comments