Mixture-of-Depths: Dynamically allocating compute in transformer-based language models

The key idea

In transformer-based language models, each token takes the same number of FLOPs to generate. However, some tokens may be harder to predict than others, and therefore it would be preferable to dynamically allocate compute across the sequence length. Mixture-of-Depths (MoD) aims to achieve this by capping the number of tokens that can participate in a given transformer layer.

Mixture-of-Depths Transformer. As in mixture-of-experts (MoE) transformers, a router chooses among potential computational paths. But unlike in MoE transformers, the possible choices are a standard block’s computation (i.e., self-attention and MLP) or a residual connection. Since some tokens take this second route, Mixture-of-Depths (MoD) transformers have a smaller total FLOP footprint compared to vanilla or MoE transformers. On the top right is depicted a trained model’s routing decisions for a short sequence truncated to 64 tokens for visualization purposes. When examining the choices one can find tokens processed by later blocks’ layers, despite passing through relatively few total blocks throughout the model’s depth. This is a unique feature of MoD compared to conventional halting-based, or "early-exit" conditional computation, which instead engage blocks serially, or vanilla transformers, which engage every block.

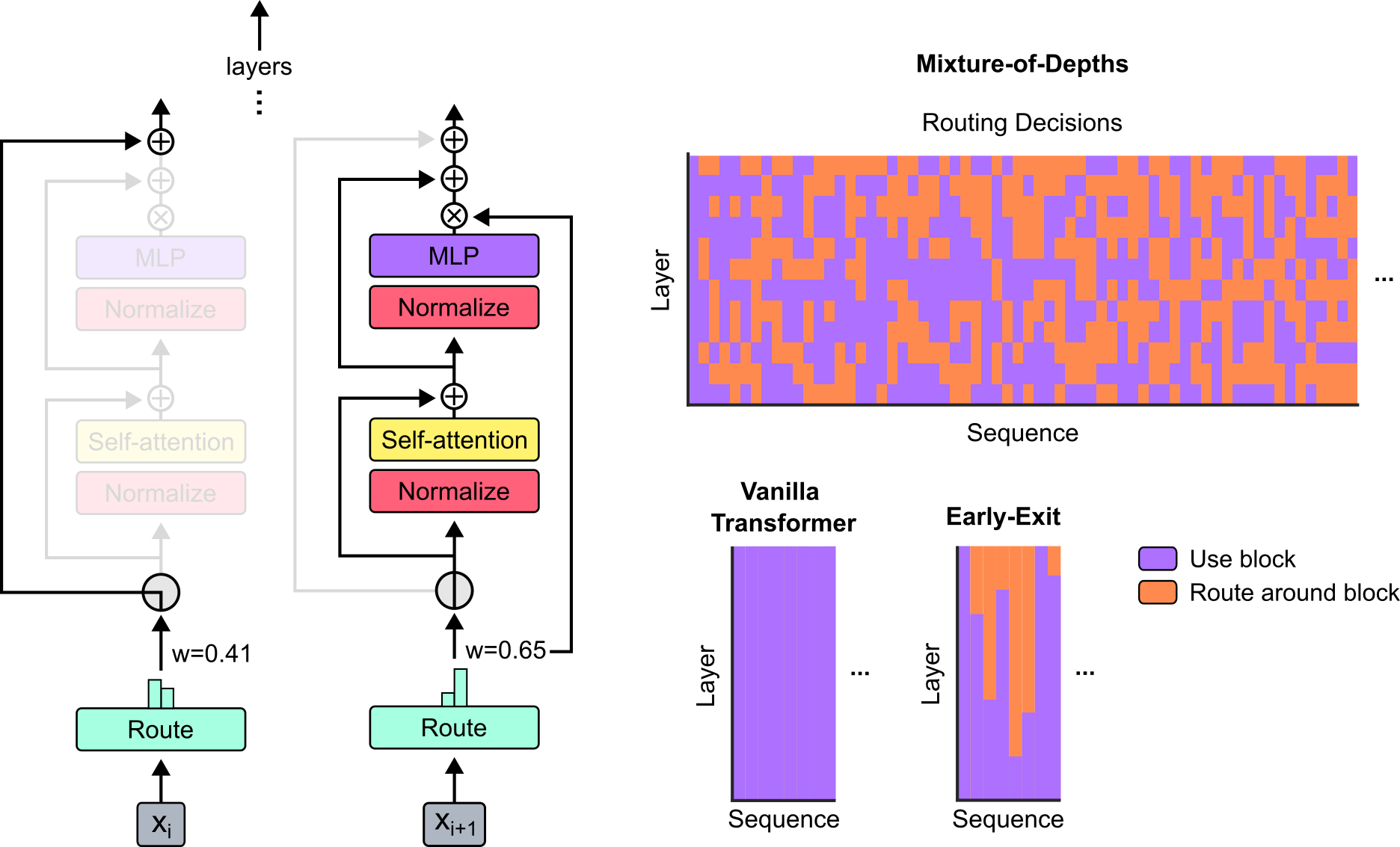
Their method

MoD sets a static compute budget which limits the number of tokens that can participate in a transformer layer’s computations (self-attention and MLP). All remaining tokens bypass the block via a residual connection. A routing mechanism is used to determine which path each token takes.

For a layer $l$ and an input sequence $\mathbf{X}^l \in \mathbb{R}^{S \times d}$ (where $S$ is the sequence length and $d$ is the model dimension), MoD includes trainable parameters $\mathbf{w}^l \in \mathbb{R}^d$ such that the linear projection $\mathbf{R}^l = \mathbf{X}_i^l \mathbf{w}^l \in \mathbb{R}^S$ are the router weights for the sequence. The tokens that correspond to the top-$k$ largest router weights (where $k$ is based on the compute budget) participate in the layer’s computations, with the remaining tokens skipping the block.

The top-$k$ operation requires knowing the router weights for all tokens, which is not possible when autoregressively sampling such as during LLM inference. The authors provide two strategies to overcome this: the first method introduces an auxiliary loss which trains the routing mechanism to output $1$ if a token is among the top-$k$, and $0$ if not. This approach does affect the primary language modelling objective but allows sampling from the model autoregressively. The second method introduces a second router (whose gradients do not backpropagate through the main model) which predicts whether a token will be among the top-$k$ or not. This approach does not affect the language modelling objective, nor does it significantly impact the step speed.

Results

isoFLOP analysis. We used the 12.5% capacity MoD variant to perform an isoFLOP analysis for 6e18, 2e19, and 1e20 FLOPs, training models varying in size from 60M to 3B parameters. Depicted on the right are the relative FLOPs per forward pass (normalized to the isoFLOP optimal baseline). There exist MoD variants that are both faster to step (by virtue of requiring fewer FLOPs per forward pass) and better performing than the isoFLOP optimal baseline.

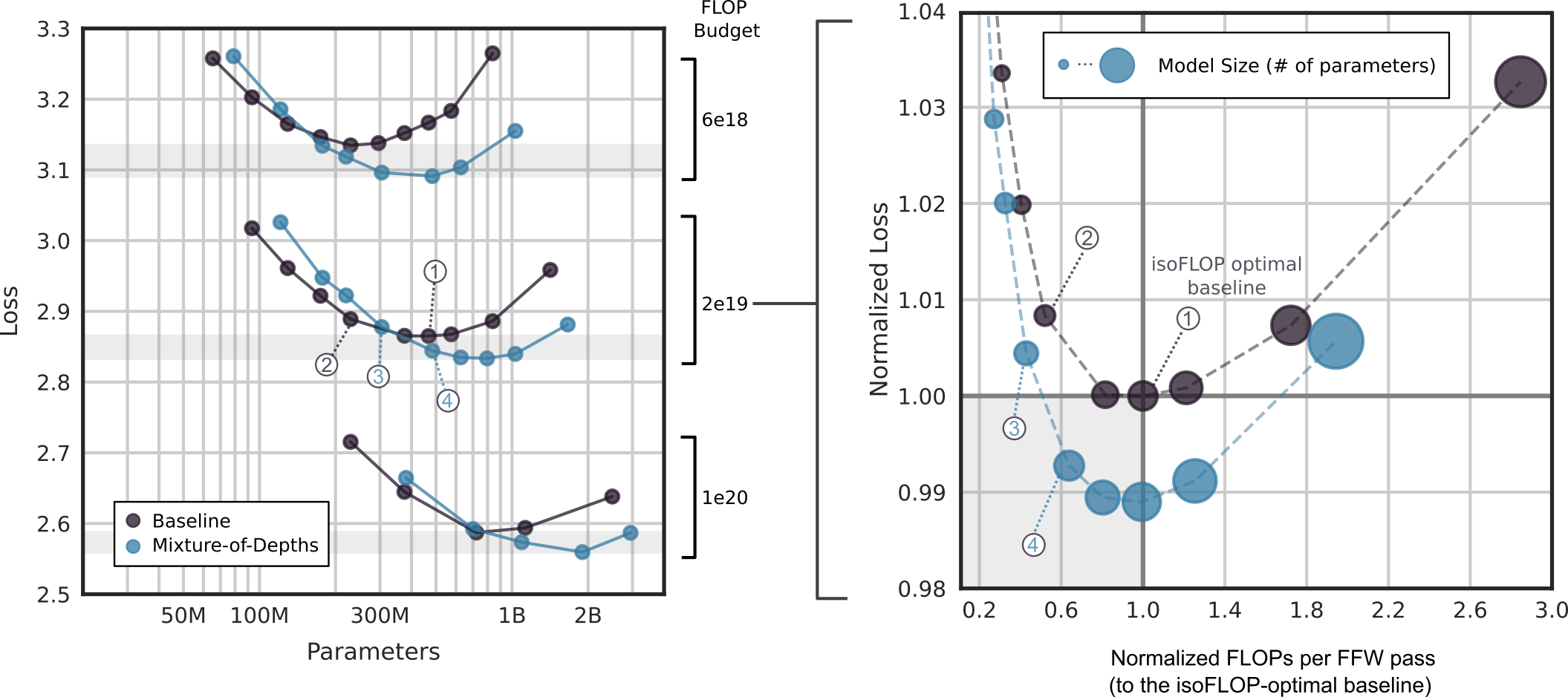
The authors compare MoD transformers against vanilla transformers trained on equivalent compute budgets (isoFLOP). The results found that MoD transformers can attain lower losses for a given training budget than their vanilla counterparts (as seen on the left of the Figure above). When comparing the FLOPs per forward pass (seen on the right of the Figure above), MoD transformers can achieve a lower loss while requiring fewer FLOPs (even for larger parameter counts), potentially making MoD a valuable approach for speeding up LLM inference while improving its task performance.

Mixture-of-Depths-and-Experts (MoDE). The MoD technique can be implemented alongside MoE (together comprising MoDE models) in two straightforward manners: staged, which first implements MoD machinery prior to MoE machinery, and integrated, which uses one routing operation to funnel tokens to either experts or no-op operations.

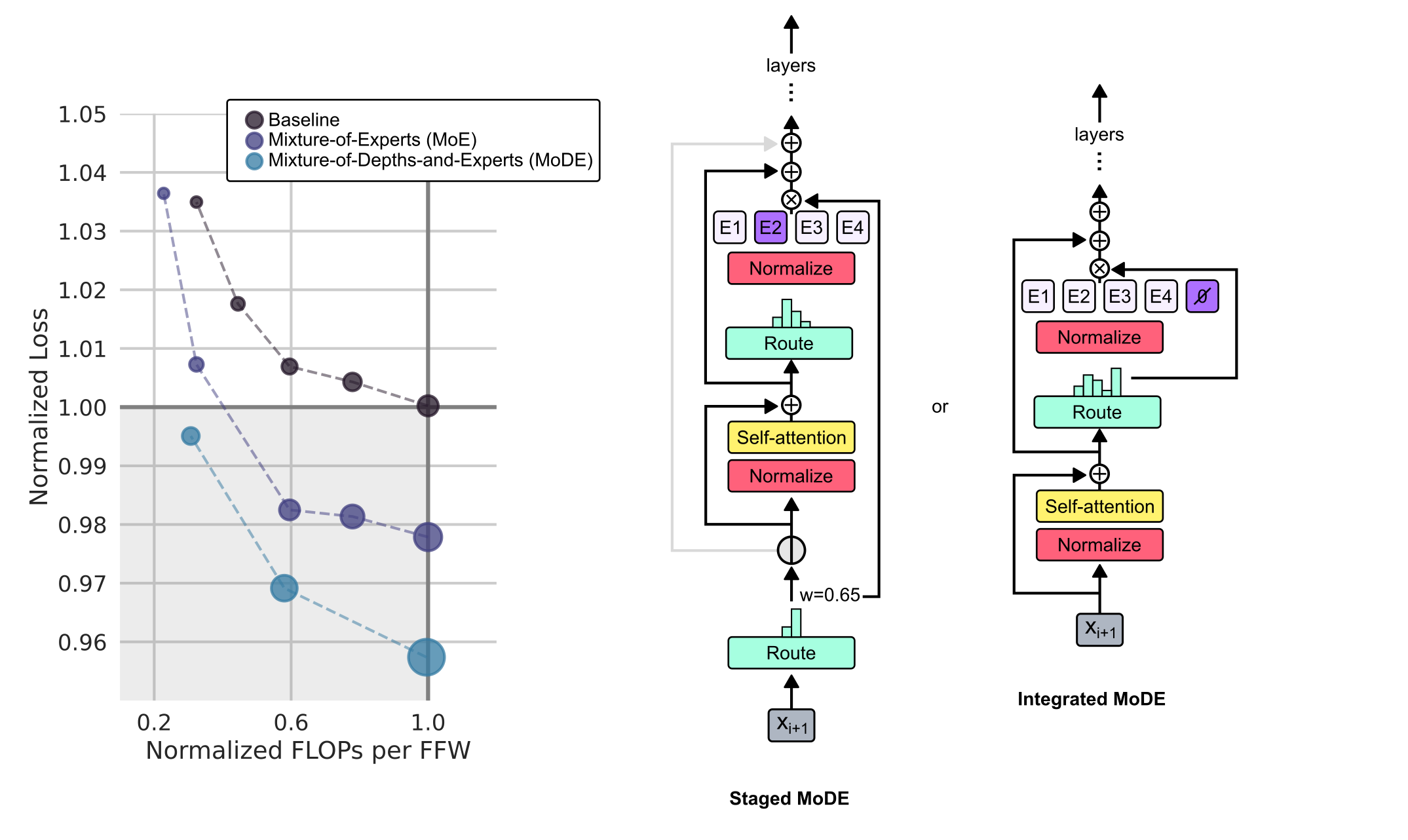
The Mixture-of-Depths approach is inspired by the analogously-named Mixture-of-Experts (MoE), as an alternative approach to conditional compute. As a final investigation, the authors combine both approaches and evaluate Mixture-of-Depths-and-Experts (MoDE), and find that it is able to outperform MoE when comparing the FLOPs per forward pass (as seen in the Figure above).

Takeaways

The Mixture-of-Depths approach unlocks a new way to increase model capacity and capability without incurring the typical compute penalties associated with model scaling. While the focus of the paper has been addressing the practical and algorithmic concerns and challenges, it would be great to see how MoD fares on a variety of downstream tasks, as it is hard to verify how useful this method would be in practice. Nevertheless, this paper is the first of hopefully many papers to come on the topic, and it will be demonstrated as a viable method for training and deploying LLMs in the wild.

---

_{Note: formulae have been adapted from the original paper.}