Solving olympiad geometry without human demonstrations

The key idea

ML approaches to mathematical theorem proving are bottlenecked by the scarcity of training data. The first contribution made by the authors is the designing of a procedure to generate a large synthetic dataset of Euclidean geometry theorem proofs by means of a traceback algorithm driven by a symbolic deduction engine.

This dataset is then used to train AlphaGeometry, a hybrid model with an LLM providing suggestions to a symbolic engine, the first computer program to surpass the average level of International Mathematical Olympiad contestants.

Background

Classic geometry proofs extensively rely on auxiliary constructions (e.g. drawing the bisector of an angle or constructing the midpoint of a line segment), on top of the constructions explicitly provided in the statement of the theorem. Symbolic deduction engines for automated theorem proving are based on hard-coded search heuristics and struggle with auxiliary constructions, which effectively introduce an infinite number of branching points in the search tree.

While LLMs, on their own, perform poorly on theorem proving (with GPT-4 having a 0% solve rate on the set of geometry problems used for benchmarking in the paper), they have shown promise in generating exogenous proof terms, such as geometric auxiliary constructions, that can be used to restrict the search space of deduction engines. However, the difficulties and costs of translating human proofs into machine-verifiable formats strongly limit the amount of data available to train or fine-tune deep-learning models.

Their method

Synthetic dataset of theorem proofs

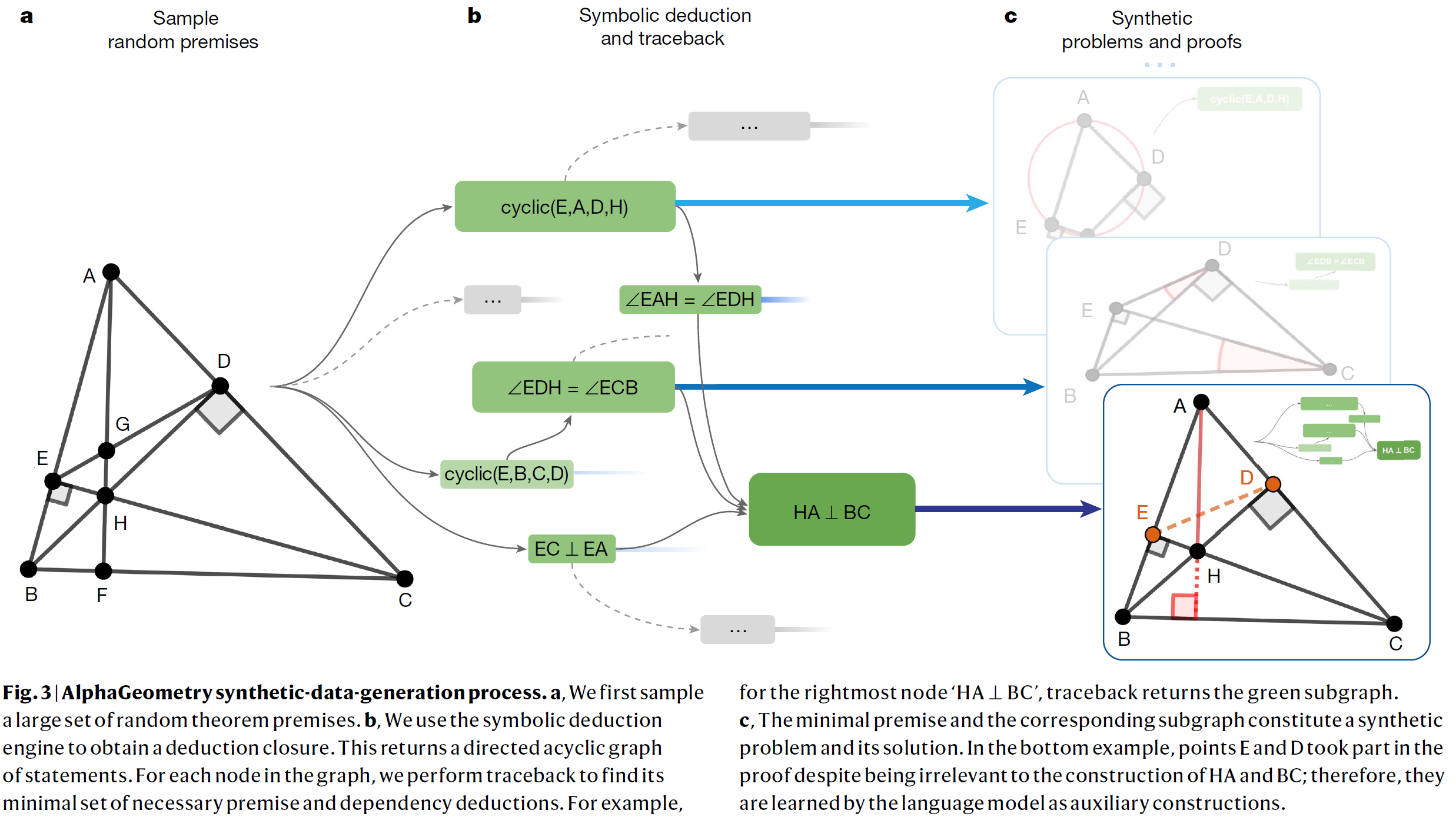
A set $P$ of theorem premises is randomly sampled and then passed to a deduction engine, which infers new statements from them using its forward deduction rules. This generates a directed graph of inferences; any node $N$ can then be seen as the conclusion of a series of logical steps represented by its dependency subgraph $G(N)$, which can be traced back to the minimal subset of premises $P(N) \subset P$ necessary to reach the conclusion.

The triple $(P(N)$, $N$, $G(N))$ is a synthetic example of a theorem, in the form (premises, conclusion, proof). The key step is then to identify auxiliary constructions among the premises $P(N)$: they are the premises that involve geometric constructions that are not necessary to state the conclusion $N$ (while being necessary to prove it!) For this reason, such premises are moved from $P(N)$ to the proof $G(N)$.

AlphaGeometry

A transformer-based language model is trained from scratch on the serialized strings ‘$P(N)$-$N$-$G(N)$’, learning to generate a proof conditioned on premises and a conclusion. Since auxiliary constructions have been moved to $G(N)$, the model crucially learns to perform them as intermediate steps in a proof.

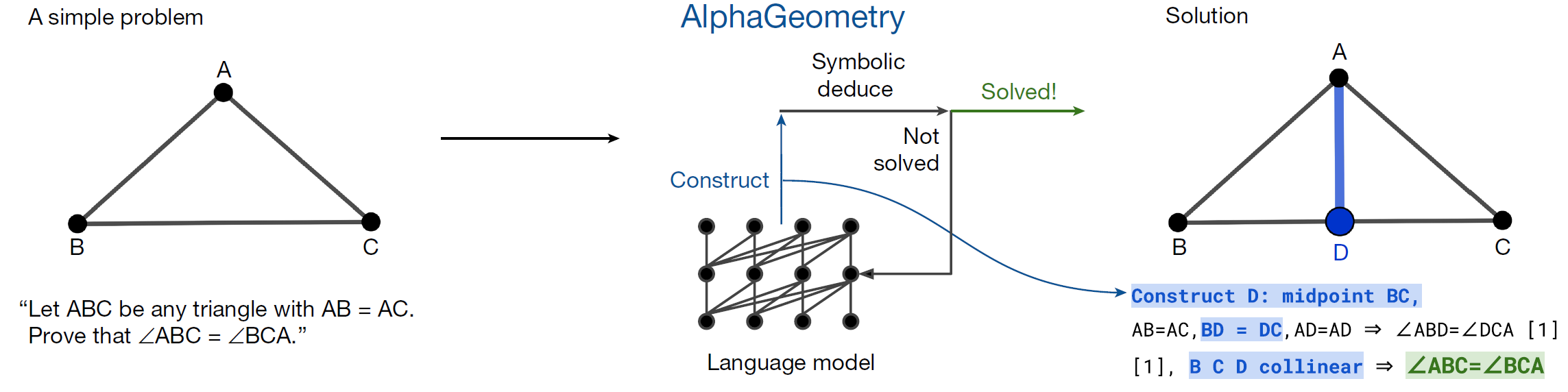
In AlphaGeometry, the resulting LLM is used to support a classical symbolic deduction engine. Whenever the engine is unable to reach the theorem conclusion, the LLM generates one sentence conditioned on the premises, all the deductions made by the engine so far and the desired conclusion. This extra sentence is passed back to the symbolic engine to expand (and steer) its search.

Results

The synthetic dataset generated by the authors contains 100 million theorems with variable proof lengths, 9% of which have auxiliary constructions. The quality of data is allegedly robust, rediscovering many non-trivial geometric theorems from the literature.

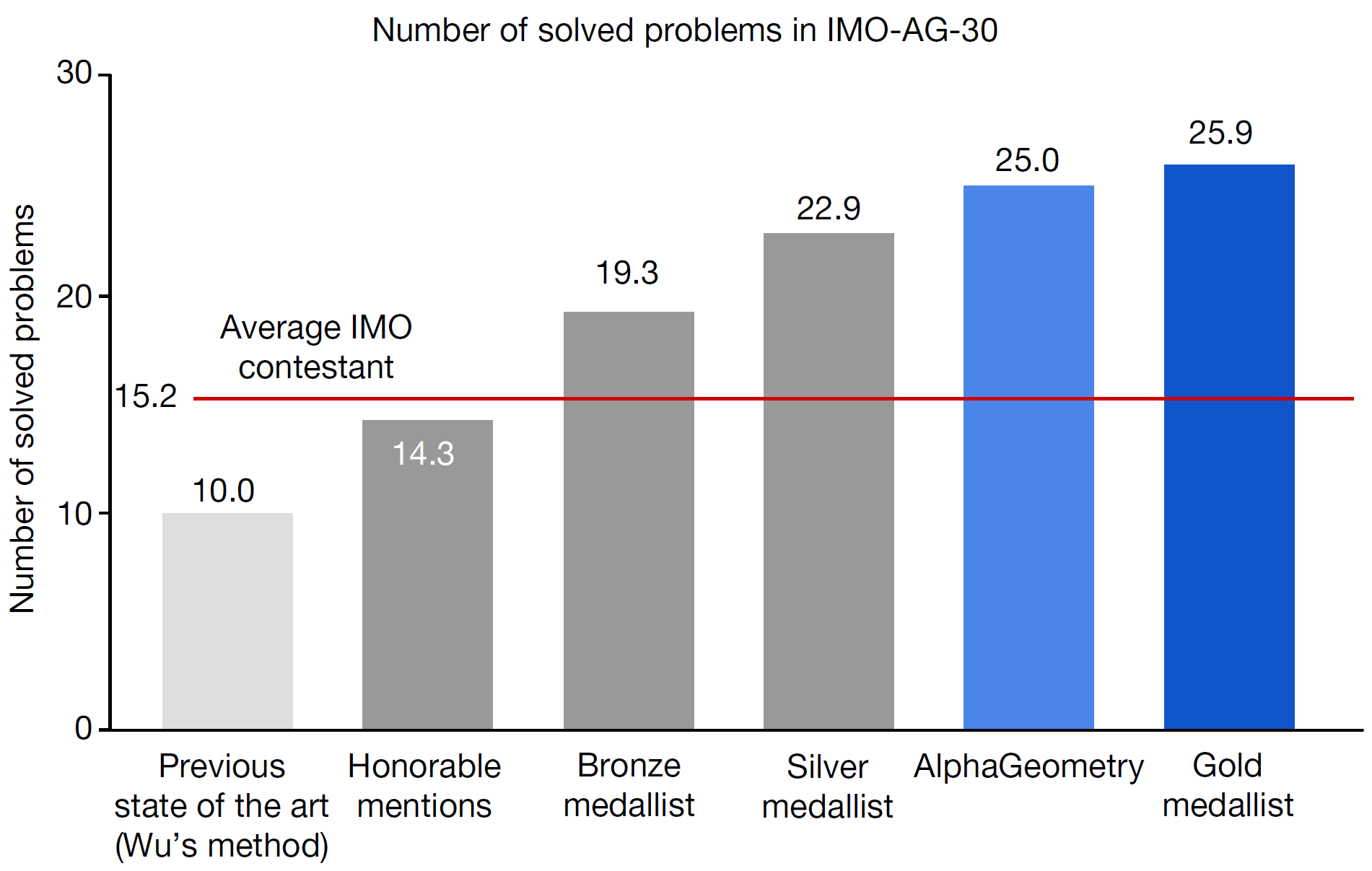
Experiments are conducted on the set of 30 plane Euclidean geometry problems from the International Mathematical Olympiad (IMO) competitions since 2000 that could be represented in a compatible format. AlphaGeometry achieves its best performance when pre-trained on the whole dataset of synthetic proofs and then fine-tuned on the subset of proofs which have auxiliary constructions, correctly solving 25 problems. This is 15 more than the previous computer algebra state-of-the-art, coming very close to the average score of a gold-medalist.

Takeaways

The paper is a brilliant example of how synthetic data can be leveraged to unleash the full power of LLMs in domains, like theorem proving and pure mathematics in general, which have been up to now more impermeable to ML advancements due to scarcity of data.