Parallel Scaling Laws for Language Models

The key idea

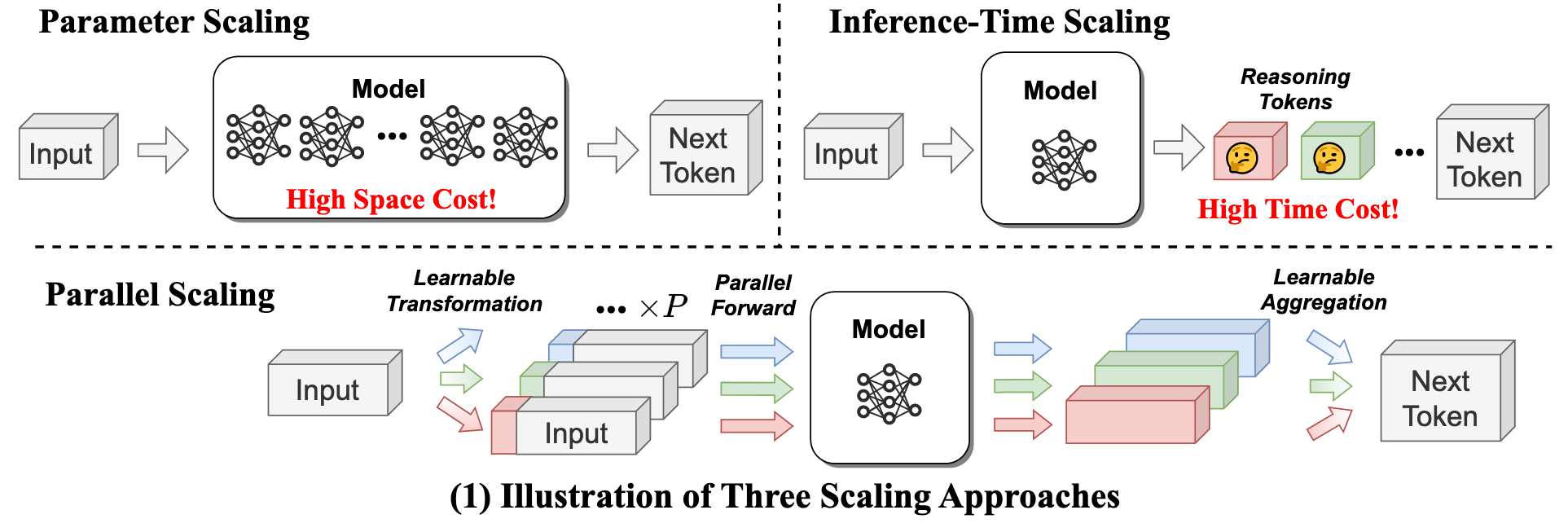
Researches at Qwen introduce a new dimension of scaling: parallel forward passes. Their method, PARSCALE, runs $P$ parallel copies of a model, each with a different learned prefix. They find that running $P$ parallel passes is equivalent to scaling the model parameters by $O(\log P)$.

Three parallel scaling approaches: Parameter, Inference time, and Parallel computation.

Background

The approach comes from a practical inference bottleneck: for large models, single batch inference can be memory-bound, especially on resource constrained edge devices. Rather than increasing model size or generating more reasoning steps, PARSCALE aims to scale a new axis, parallel computation, to keep model size approximately constant while improving performance.

Inspired by techniques like Classifier-Free Guidance (CFG), PARSCALE hypothesizes:

Scaling parallel computation (while maintaining the nearly constant parameters) enhances the model’s capability, with similar effects as scaling parameters.

Methodology

PARSCALE executes $P$ forward passes in parallel, each conditioned with a unique learned prefix (implemented via prefix tuning). Outputs of the different streams are combined using a learned aggregation MLP.

Unlike inference-time tricks (e.g., beam search or self-consistency), PARSCALE learns the aggregation during training, leading to more effective use of parallel compute. Conceptually this is similar to ensembling, but with almost complete parameter sharing between the members.

Training Strategy

To reduce training costs, they propose a two-stage approach:

• Stage 1: Standard pre-training (1T tokens)
• Stage 2: Add PARSCALE (20B tokens, 2% overhead)

Dramatically reduces cost of parallel scaling training (which requires $P$ forward passes) only applied to the final 20B tokens, not the full 1T.

Results

PARSCALE results: Parameter, Inference time, and Parallel computation.

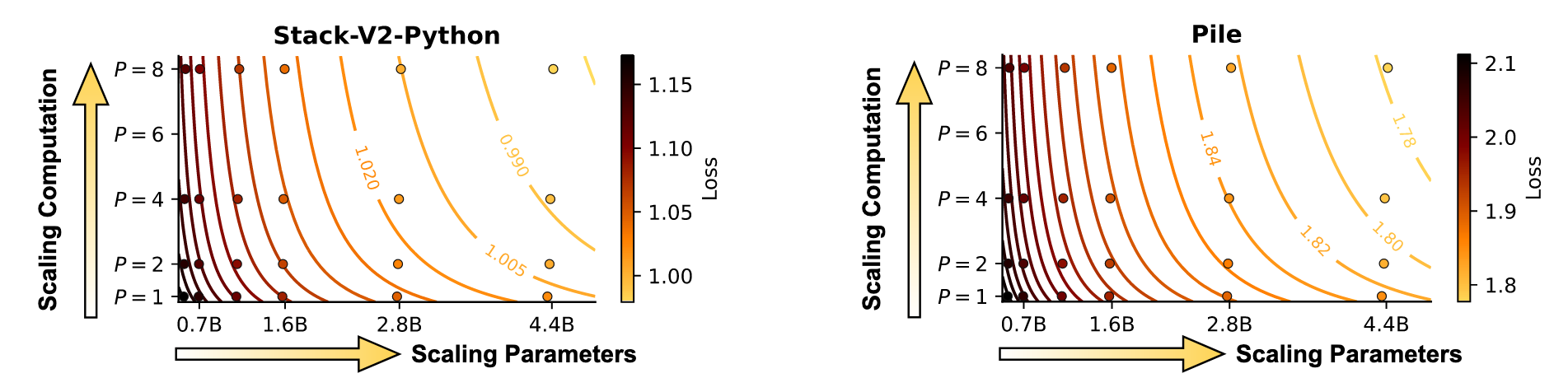
Coding Tasks (Stack-V2-Python)

Model Params	P	HumanEval+ (%)
1.6B	1	33.9
1.6B	8	39.1
4.4B	1	39.2

General Tasks (Pile)

Model Params	P	Avg Score (%)
1.6B	1	53.1
1.6B	8	55.7
2.8B	1	55.2

For a 1.6B model, scaling to $P=8$ parallel streams achieves performance comparable with a 4.4B model on coding tasks. These efficiency gains are most pronounced at small batch sizes ($\leq 8$) where inference is memory-bound. This makes PARSCALE most suitable for edge deployment scenarios.

• 22x less memory increase compared to parameter scaling.
• 6x lower latency.
• 8x increase (linear with $P$) KV cache size.

Dynamic Parallel Scaling

PARSCALE remains effective with frozen main parameters for different values of P. This enables dynamic parallel scaling: switching P to dynamically adapt model capabilities during inference.

Takeaways

PARSCALE provides a new axis in which to boost model capability, particuarly in resource constrained single-batch inference. However KV cache grows linearly with the number of parallel streams ($P$) so effectiveness may diminish beyond $P=8$ (the largest tested configuration). It is an open question as to whether $O(\log P)$ scaling holds for $P ≫ 8$.