Planned Diffusion

The key idea

Planned diffusion introduces a hybrid approach combining the strengths of autoregressive and diffusion models. First, the model autoregressively generates a plan, breaking the task into semantically independent spans. Second, the model generates these spans in parallel via discrete diffusion.

Method

In the first stage, the model sequentially generates a plan $z = (z_1, z_2, \ldots, z_N)$ given an initial context $c$ (user prompt or any previously generated tokens). It specifies a set of $b(z)$ semantically independent spans as well as the length of each span $l_k(z)$, $k \in {1, \ldots, b(z)}$. During the diffusion phase, the sequences $x(k)$ corresponding to each span $k \in {1, \ldots, b(z)}$ with $|x(k)| = l_k(z)$ are generated in parallel. The full joint distribution given context $c$ is defined as

$$p_{PD}(x, z \mid c) = p_{AR}(z \mid c) p_{D}(x \mid z, c) = p_{AR}(z \mid c) \prod_{k=1}^{b(z)} p_{D}(x(k) \mid z, c),$$

where $x = \bigcup_{k=1}^{b(z)} x(k)$, and $p_{AR}$ and $p_{D}$ denote, respectively, the auto-regressive distribution of the planning stage, respectively the distribution of the discrete diffusion model in the diffusion stage.

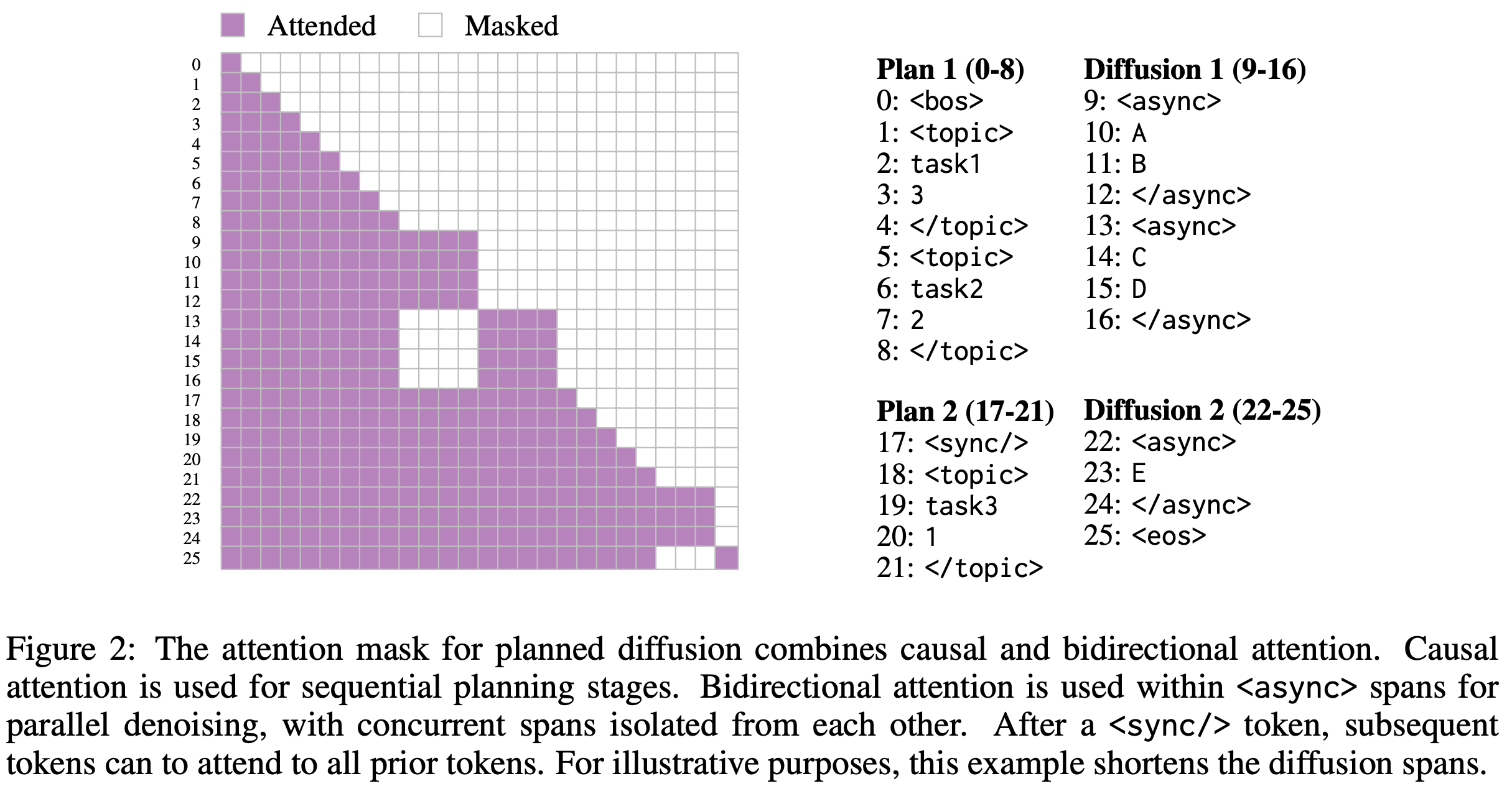
Training and special attention masking

The training loss combines an autoregressive loss and a discrete diffusion loss. More specifically, given a sequence $Y$ decomposed into sets of planning tokens $Z$ and content tokens $X$, such that $Y = Z \cup X$, and a model $f_\theta$ parameterized by $\theta$ with masking function $M_i$, the overall loss is defined as:

$$\mathcal{L}(\theta) = \underset{\underset{t \sim U(0,1)}{Y \sim \mathcal{D}}}{\mathbb{E}} \frac{1}{|\mathcal{Y}|} \sum_{y_i \in \mathcal{Y}} \Big[ \mathbb{1}(y_i \in Z), CE\big(f_\theta(y_{<i}, i), y_i\big) • \frac{1}{t}, \mathbb{1}(y_i \in X), CE\big(f_\theta(M_i(Y_t), i), y_i\big) \Big]$$

where $Y_t = X_t \cup Z$ and $X_t$ denotes the noised sequence under the discrete diffusion process. The first term in the sum corresponds to the autoregressive loss, while the second term corresponds to the diffusion loss.

Data

A synthetic data curation pipeline produces training data annotated with planning control tags, using Gemini to label the SlimOrca instruction-finetuning dataset.

Inference

Several techniques are used to improve sampling performance and efficiency: variable-length denoising, where the number of denoising steps depends on the length of the longest span; KV caching; and entropy-ordered unmasking.

Results

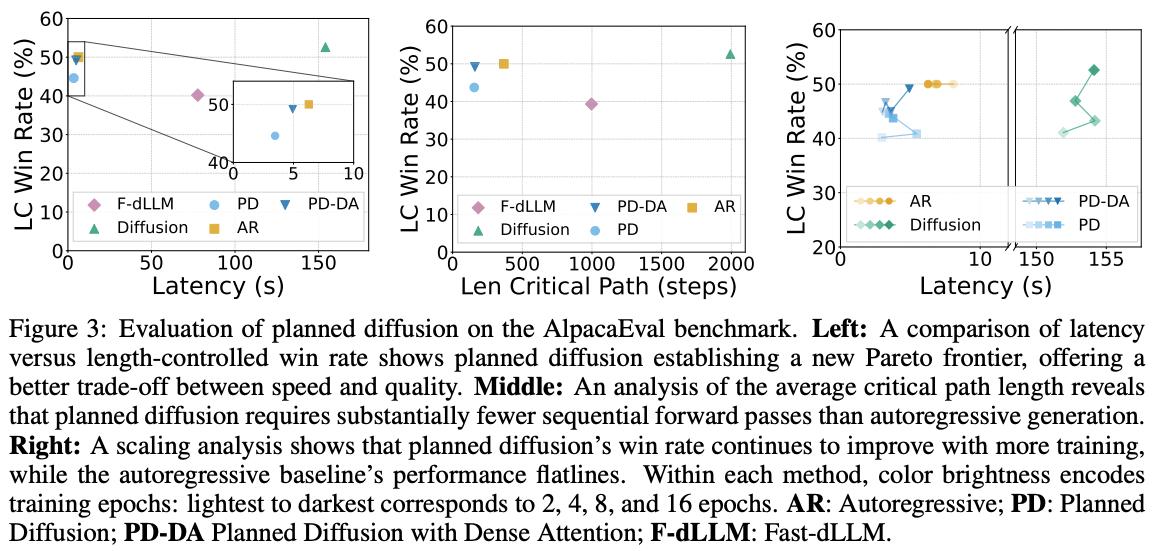
The base model is first pre-trained autoregressively and then further pre-trained with a diffusion objective. It is subsequently fine-tuned on the synthetic dataset using four decoding strategies: autoregressive, diffusion, Fast-dLLM, and Planned Diffusion. Planned Diffusion demonstrates promising improvements by establishing a new latency–quality Pareto frontier, achieving up to ~1.8× faster decoding compared to standard autoregressive generation, and continues to improve with additional training, whereas the autoregressive baseline plateaus. However, these gains come at the cost of a small decline in LC win rate, reflecting a minor trade-off in instruction-following quality for reduced latency.