QuaRot: Outlier-Free 4-Bit Inference in Rotated LLMs

The key idea

As large language models (LLMs) are getting increasingly used in many applications, efficient inference (in terms of memory, compute and energy) is a dynamic research field. In this domain, quantisation of models is the predominant technique, as it improves efficiency on all three axes simultaneously: reducing the memory usage for weights and KV cache, and improving compute time (and energy use) by lowering the precision of matrix multiplication.

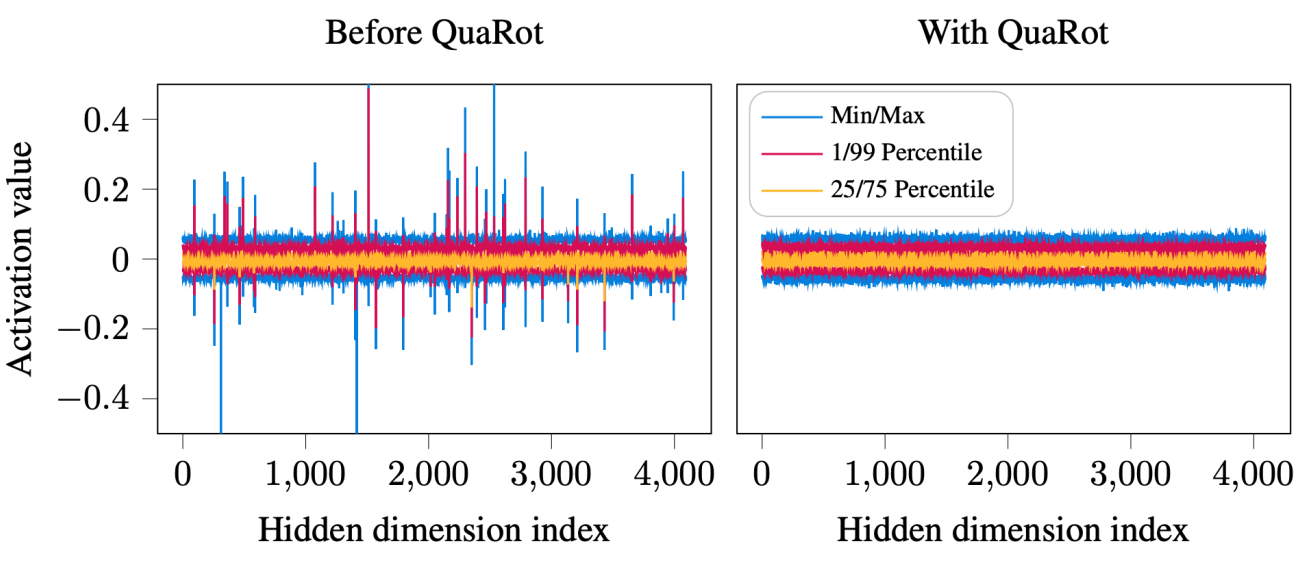
Nevertheless, one major issue in the LLMs quantisation literature has been how to efficiently handle activation outliers while retaining model accuracy. The QuaRot work presents an elegant way of modifying a pre-trained (frozen) LLM to remove outliers in the distribution of activations, opening the door to accurate and efficient 4-bit weights, activations and KV cache inference.

Background

In LLMs quantisation, weights and activations are not born equal. A large literature initially looked at weights quantisation only, leaving activations and matrix multiplication in 16-bit formats. Quantisation of LLMs activations happens to be more challenging as they display large outliers, contrary to weights. As a consequence, a popular quantisation approach has been to represent activation tensors in 4/8 bits, but also keep track of the set of largest outliers in 16-bit (e.g. LLM.int8, QUIK). While accurate, this type of mixed representation method tends to have sub-optimal compute performance for LLM inference.

Their method

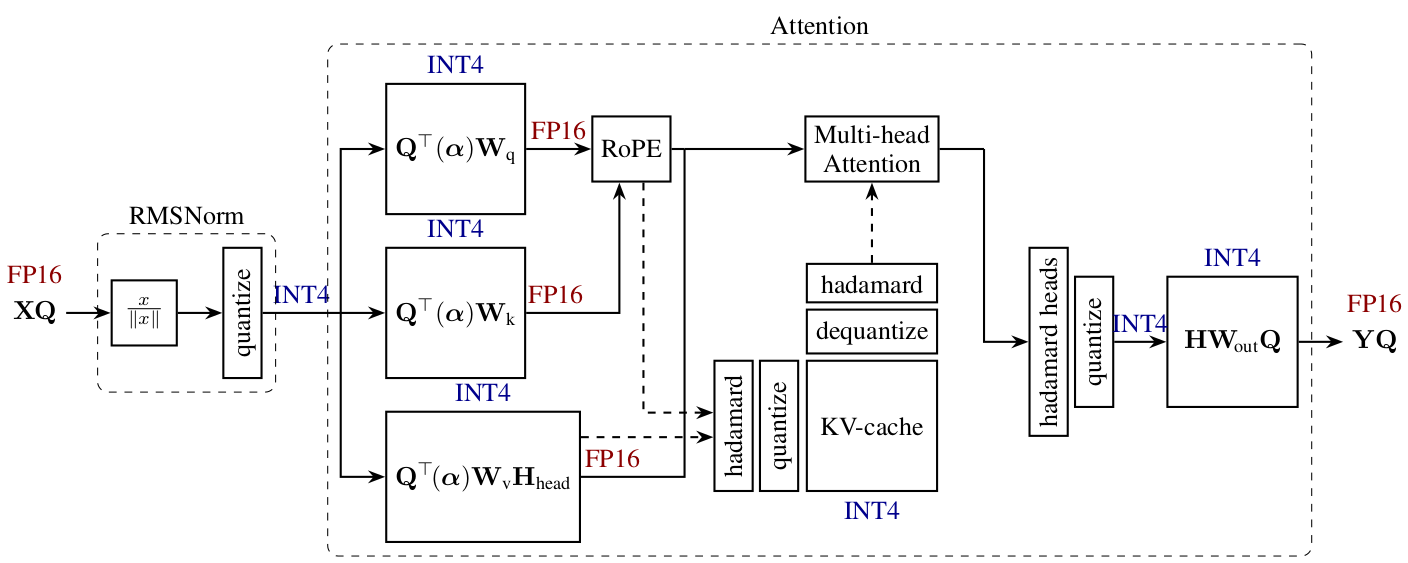
QuaRot aims to tackle the 4-bit quantisation of activations (and KV cache) by modifying the model definition, adding Hadamard transforms to the attention and linear modules, smoothing in this way the distribution of activations and removing outliers.

Distribution of activations in Llama pre/post QuaRot.

The Hadamard transforms $H$ have been popular in a few recent publications, as they present the benefit of random orthogonal matrices for “smoothing” tensor distribution while being very cheap and fast to compute on GPUs (a matrix-vector product $Hx$ requiring only $\text{O}(d\,\text{log}(d))$ operations). In short, Walsh-Hadamard transforms are defined recursively by:

$$ H_2 = \tfrac{1}{\sqrt{2}}\left[\begin{array}{cc} 1&1\\1&-1\end{array}\right] \quad\textrm{and} \quad H_{2^n} = H_2 \otimes H_{2^{n-1}}, $$

and randomized Hadamard can be easily generated by combining the later with a diagonal matrix of random draws in ${+1, -1}$.

As presented in the paper (see figure above), integrating Hadamard transforms to the attention and FFN components removes outliers from the distribution of activations in LLMs such as Llama, improving as a consequence quantisation of these models. Additionally, most of these Hadamard transforms can be directly fused into model weights, or commuted with the RMSNorm, leaving only $1\tfrac{1}{2}$ per transformer layer to be computed for online LLM inference.

QuaRot integration of Hadamard transforms in the attention layer.

Results

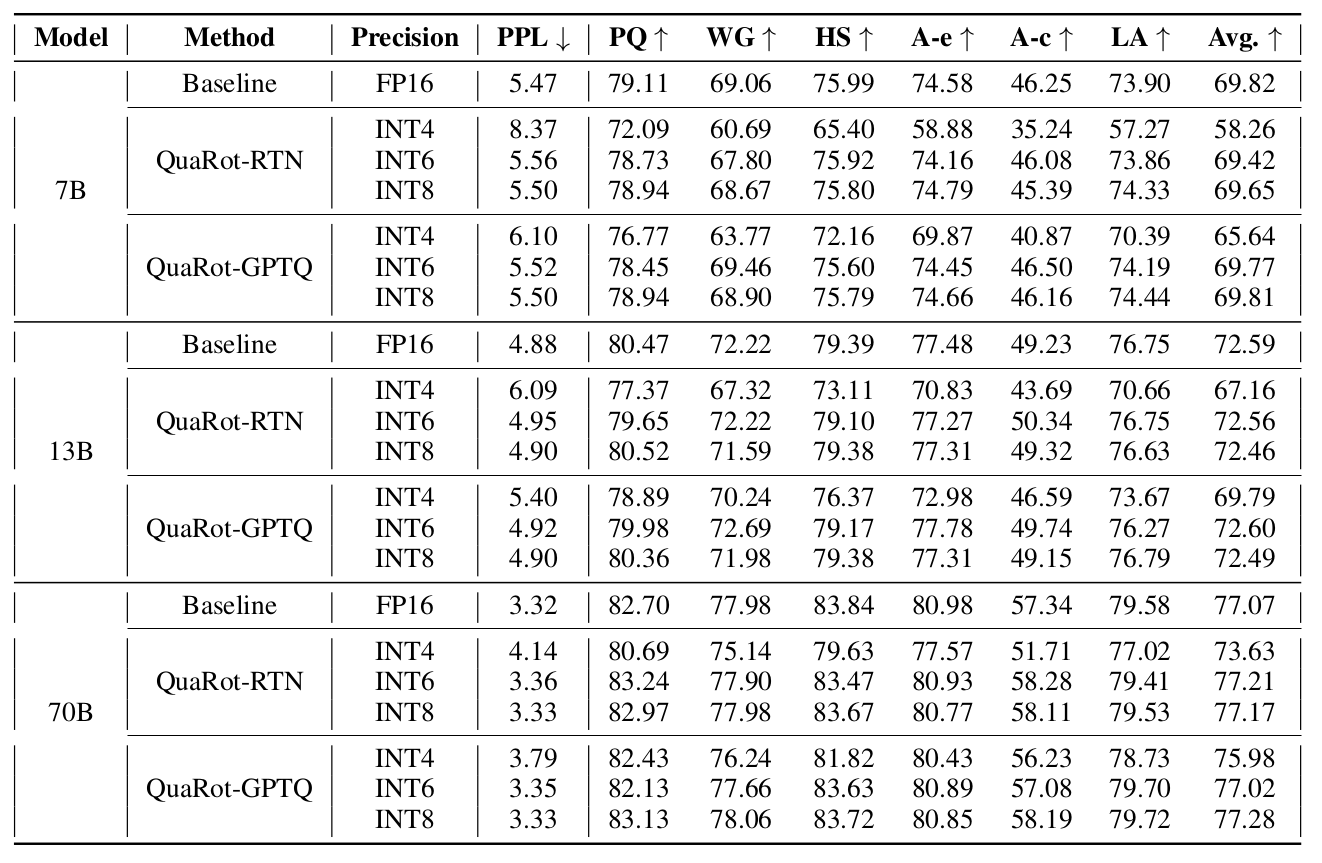
QuaRot shows strong results in terms of accuracy and performance, across different sizes of Llama models (7B, 13B and 70B). Associated with GPTQ, 6-bit and 8-bit QuaRot quantisation matches 16-bit accuracy on multiple benchmarks, while 4-bit quantisation presents only minor accuracy degradation. Additionally, it is shown that the additional Hadamard transforms only have a 7% overhead as they can be efficiently fused with 4-bit GPU GEMM kernels. Interestingly, we note that round-to-nearest (RTN) is matching the more complex GPTQ quantisation technique as models are getting larger.

Llama post-training QuaRot quantisation, using round-to-nearest or GPTQ.