QuIP#: Even Better LLM Quantization with Hadamard Incoherence and Lattice Codebooks

The key idea

Enable extreme compression by transforming weights to something less heavy-tailed before quantising with a set of spherical (rather than grid-like) codes!

Background

LLM token generation is memory-bandwidth bound, i.e. limited by the rate at which model state can be read. This means that any reduction in #GB to store model weights and KV cache can increase #tokens/sec.

Widely adopted LLM compression techniques typically stop at 4-bits since this hits a sweet spot with

1. very little degradation in downstream task performance
2. element-wise codecs that are straightforward to parallelise and optimise on modern hardware.

One reason these techniques struggle to quantise to fewer bits is that the tails of LLM weights and activations distributions affecting the majority of computation become increasingly susceptible to quantisation error. To address this, the authors previously proposed QuIP in which weights are transformed to have a less heavy-tailed distribution. Here they present two key improvements to QuIP.

Their method

QuIP is comprised of two key components:

1. A transform using orthogonal matrices $U$ and $V$ used to convert weights $W$ and layer activations $x$ such that $\tilde{W} = U^TWV$ and $\tilde{H} = V^THV$ where $H$ is a proxy Hessian of layer activations $H=\mathbb{E}[xx^T]$.

2. A quantisation algorithm $Q$ that maps $\tilde{W}$ to some quantised space in such a way that minimises quantisation error of outlier activations.

Which you can summarise with:

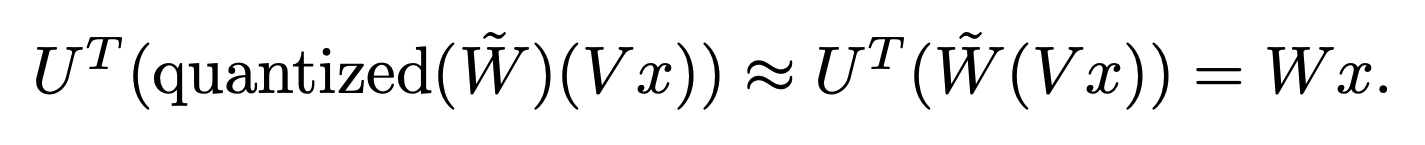
QuIP# improves both the method for generating $U$ and $V$ and the quantisation algorithm $Q$.

$U$, $V$ generation: To exploit GPU parallelism and decrease bounds on outlier features, the authors propose using a Randomised Hadamard Transform (RHT), in which U and V can be represented as Hadamard matrices along with randomly generated sign flips of weight columns. They prove that the largest singular values of transformed weight matrices scale logarithmically with the size of the weight matrices, meaning lower probability of outliers in weights needed to be quantised.

Q algorithm: As with other recent methods (e.g. AQLM, GPTVQ), the authors explore vector quantisation as a means to provide a high-density quantised space to map uncompressed points onto. The key idea behind vector quantisation is that you can define arbitrary prototypes to discretise a multi-dimensional space, rather than regular grid-like points that would result from elementwise, scalar quantisation. A key choice for any vector quantisation algorithm is the set of prototypes, or codebook $C$ that is used to discretise the space. Here the authors choose the E8-Lattice, since it has both high packing density in multi-dimensional space and can be exploited for symmetries to compress further. Choices on how to combines sets of lattices define the #bits a vector is compressed to.

Results

Compressing to 3-bits introduces very little degradation in perplexity compared to an FP16 baseline. So much so that it looks like the trade-off of using a slightly larger model compressed to fewer bits is worthwhile.

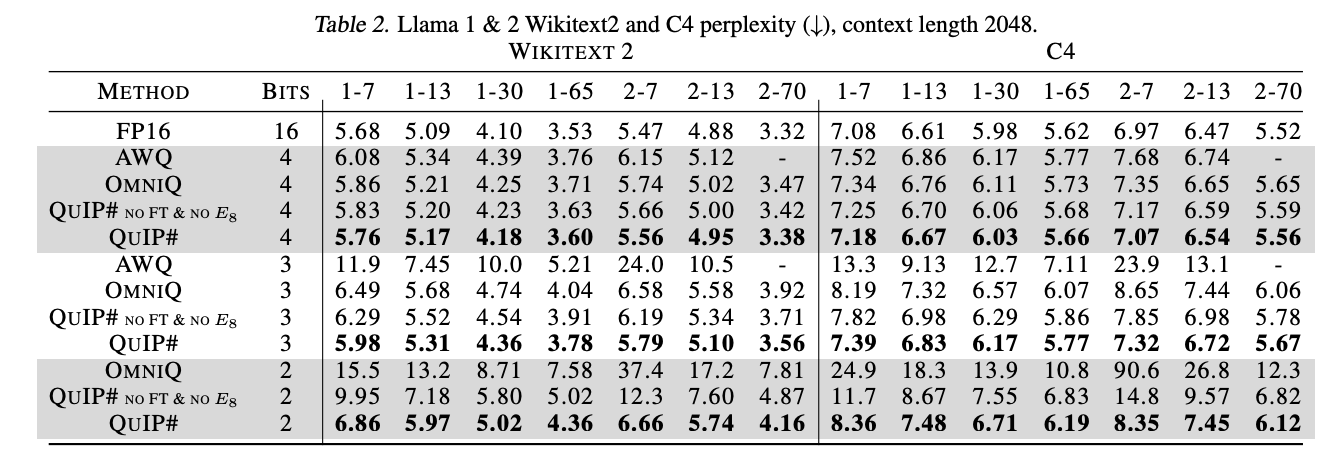
It’s worth noting that the perplexity gains over AQLM are only realised if you use both the lattice codebook and finetune.

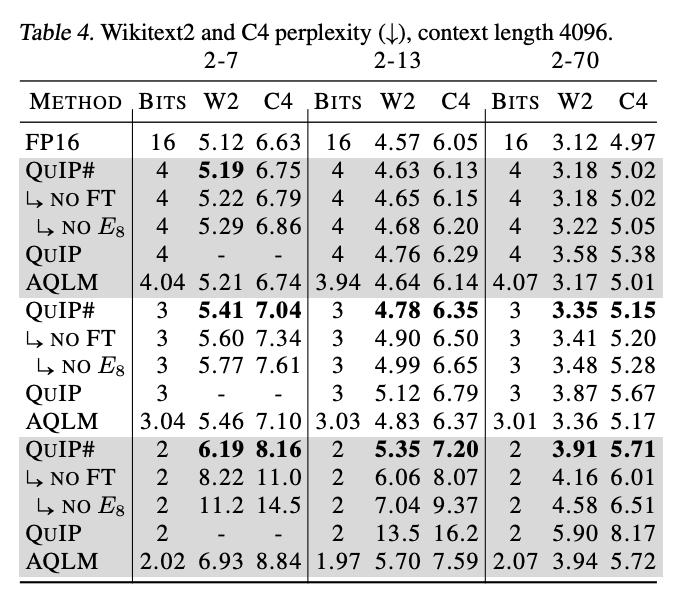
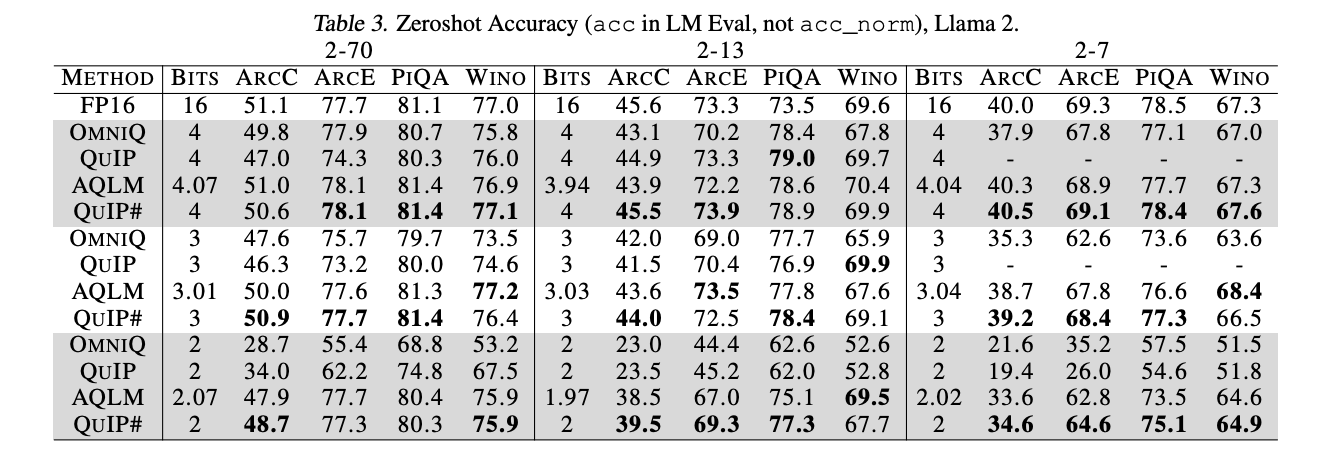
As is often the case, low perplexity doesn’t always translate to better zero-shot performance on typical QA tasks, although it looks as though QuIP# stands up well in many cases.

In terms of practical speed-ups that can be gained from using this, a lot seems to depend on how efficiently the Randomized Hadamard transform and lookups into the E8-lattice can be implemented. Both are memory bandwidth bound operations, but might also be difficult to achieve peak bandwidth. Notably, the authors don’t publish #tokens/sec for their eye-catching 3-bit compression scenario, only 2- and 4-bit.

Takeaways

This is a compelling proof-of-concept that 3-bit compression can be effective work. Concurrent work also seems to suggest that vector quantisation is critical for sub 4-bit compression, although it remains to be seen how practical speedups can be realised (even in other works). It is also worth noting that GPTVQ (published within the last week) appears to obtain better 3-bit perplexity results for larger models than QuIP#. This promises to be an exciting race to find the best schemes with suggestions for how future low-precision hardware might look!