How to Scale Second-Order Optimization

The key idea

Now we know that optimizers like Muon can train LLMs more efficiently than Adam, let’s learn how to tune them for optimal efficiency. That will show us the difference between well-tuned Adam and well-tuned second-order optimizers.

Background

Throughout a decade of transformation in deep learning, Adam dominated as the de facto default optimizer of choice for neural network training. Although there have been many and various optimizers proposed, Adam’s combination of momentum and normalized gradients with per-parameter adaptivity has proven hard to beat. However, this status quo is being challenged: Muon was shown to be the most efficient optimizer for training LLMs in the nanogpt speed-run, and then scaled up successfully to 16B-parameter models. In this context comes How to Scale Second-Order Optimization, presented at NeurIPS 2025 in San Diego last week.

The key idea in this paper is to analyse the hyperparameters and scaling laws that are applied with second-order optimizers, to find best practice for these new optimizers rather than simply reusing the rules and patterns that have proven to be successful for Adam.

The paper presents several key findings:

1. They derive the maximal update parameterization ($\mu P$) for second-order optimizers to transfer learning rate and other hyperparameters from small-scale runs. This includes a recommended scaling factor of $1/L$ for residual blocks in $L$-layer transformers, as per ‘CompleteP’.
2. They show that under ‘compute-optimal’ training, following scaling laws like Chinchilla’s 20 tokens per parameter, the weight decay parameter $\lambda$ should be scaled inversely to the model depth $D$, so that $\lambda D$ is roughly constant.
3. They show that the optimal number of tokens per parameter is smaller for Muon: they find ~7 tokens per parameter to be compute-optimal for Muon and 11-14 for Adam. If holding the total training compute fixed, this means that we can train a larger/wider model with Muon than we can with Adam, leading to lower loss overall.

Results

Taken together, these recommendations show that well-tuned Muon can train LLMs with 1.4x less compute than a well-tuned Adam run requires to reach the same loss.

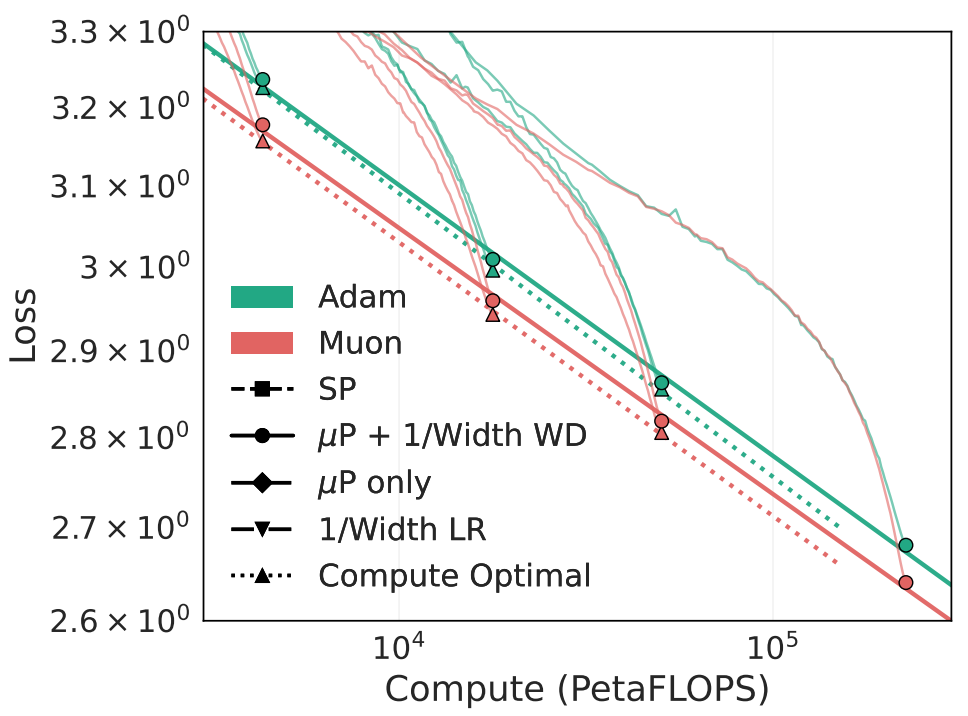
This figure from the paper shows Adam compared to Muon for training LLaMA-architecture LLMs at 190M-1.4B parameters. The ‘Compute Optimal’ curves (with triangle markers) use fewer tokens per parameter, so the fixed compute budget can be deployed to widen the model architecture, thus leading to lower loss compared to the runs with 20 tokens per parameter (with circle markers). For example, the smallest compute-optimal Adam run, at ~$6 \times 10^{16}$ FLOPs, uses model width of 576, whereas the Muon run uses a width of 704. Note that the NeurIPS review discussion suggests that the FLOP count excludes the additional compute required for the Muon optimizer steps, which the Muon blog post estimates as an overhead of below 1% total FLOPs.

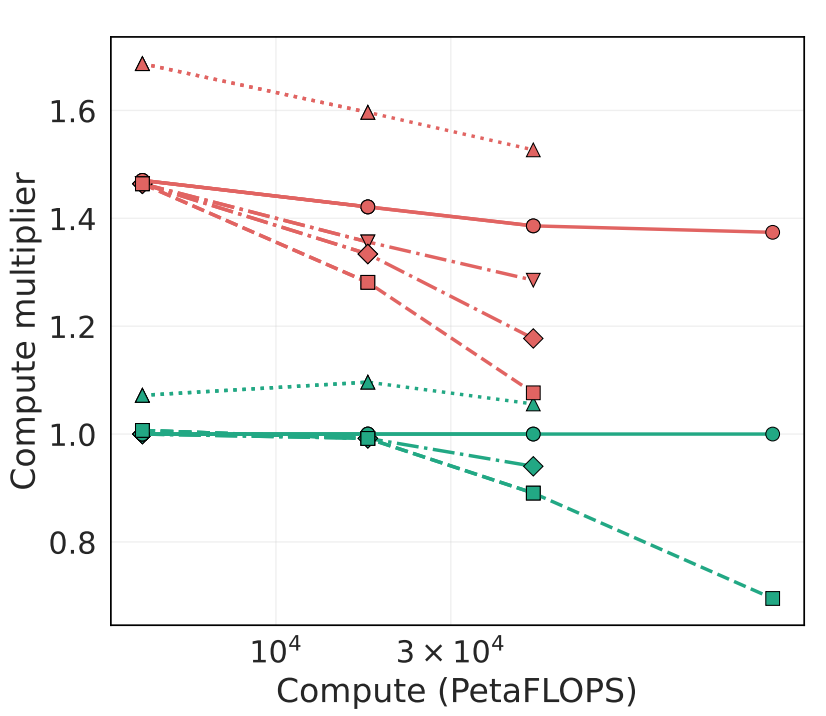
This plot corresponds to the graph above, and ablates each of the recommendations in the paper, showing the reduction in compute for Muon compared to Adam under their recommended scaling rules. The key takeaway is that when scaled correctly (circle markers), Muon maintains a constant 1.4x reduction in compute compared to Adam. Less-careful deployment of Muon (e.g. in the SP runs with square markers) leads to much smaller reductions in compute at larger model scale, reaching as little as a ~1.1x advantage for models at ~640M parameters.

Takeaways

• Second-order optimizers have a real and practical advantage over Adam for training LLMs at a range of model scales.
• Getting optimal efficiency from new optimizers requires some care: if we just swap out Adam for Muon, we’re leaving potential efficiency gains on the table.