SOAP: Improving and Stabilizing Shampoo using Adam

The key idea

It turns out that the Shampoo optimiser (explained below), with some minor tweaks, is equivalent to running Adafactor in Shampoo’s eigenspace. Since Adafactor is a rank=1 variant of Adam, the proposed method “SOAP” runs Adam in Shampoo’s eigenspace instead.

Figure 1. SOAP performance versus Adam and Shampoo, showing good step-efficiency (due to Adam) and time-efficiency (due to periodic preconditioning). Less frequent preconditioning hurts Shampoo more than SOAP.

Background

Shampoo for matrices looks like this:

$$\begin{aligned} L_t &= L_{t-1} + G_t G_t^{\top} \\ R_t &= R_{t-1} + G_t^{\top} G_t \\ W_t &= W_{t-1} - \eta \cdot L_t^{-1/4} G_t R_t^{-1/4} \end{aligned}$$

Where $W \in \Re^{m \times n}$ is a weight matrix, $L\in \Re^{m \times m}$, $R\in \Re^{n \times n}$ are “preconditioners”, behaving a bit like optimiser state and $G$ is the minibatch gradient of a loss with respect to $W$.

A slightly different variant is considered here: idealised Shampoo with power $1/2$,

$$\begin{aligned} L &= \mathbb{E}(G G^{\top}) \\ R &= \mathbb{E}(G^{\top} G) \\ W_t &= W_{t-1} - \eta \cdot L^{-1/2} G_t R^{-1/2} \,/\, \mathrm{tr}(L) \end{aligned}$$

Note that this idealised variant takes an expectation over gradients from the dataset, rather than a running average as per practical implementations. The authors show that the last line is equivalent to idealised Adafactor in the Shampoo eigenspace:

$$\begin{aligned} Q_L &= \mathrm{Eigenvectors}(L) \\ Q_R &= \mathrm{Eigenvectors}(R) \\ G^{\prime} &= Q_L^{\top} G Q_R \\ W_t &= W_{t-1} - \eta \cdot Q_L^{\top} \mathrm{Adafactor}(G^{\prime}) Q_R \end{aligned}$$

Their method

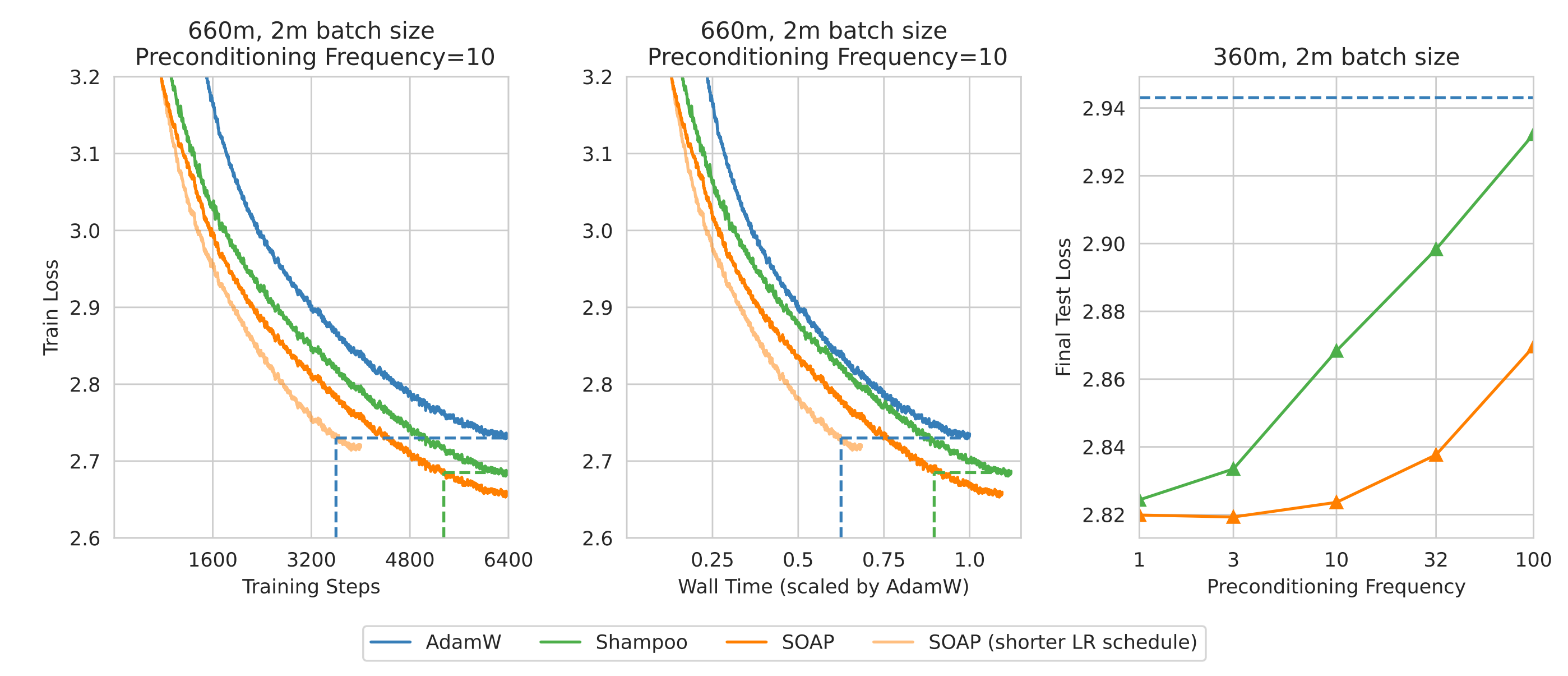
Based on this link between Shampoo and Adafactor, the authors propose SOAP, which runs full Adam in the Shampoo eigenspace and increases efficiency by only updating the eigenvectors periodically (e.g. every 10 steps).

The running state of this technique includes $L$, $R$, $Q_L$, $Q_R$, $M$ (in the weight space) and $V$ (in the Shampoo eigenspace). For large projections, such as the final projection layer in an LLM, the corresponding $Q_L$ or $Q_R$ can be fixed to identity. If both are fixed, SOAP reproduces Adam.

Results

Results on language modelling (see figure above) show good step-efficiency of SOAP since it is based on Adam rather than Adafactor, and time-efficiency since the eigenvectors can be periodically updated without substantially harming performance. Like Shampoo, the extra optimisation cost can be reduced by using a large batch size.

Stepping back for a moment, I’m excited about this progress using Shampoo variants and am eager to see experiments over long training runs of LLMs. So I hope we’ll see plenty more shower-related puns on arXiv over the next year!