Soft Tokens, Hard Truths

The key idea

Over the course of the last year, a number of works have investigated “latent reasoning”, in which reasoning tokens are represented in some continuous latent space, rather than a specific token in the language vocabulary. Many of these works require implementation schemes that are difficult to scale (such as Coconut) or are training-free (such as Soft Thinking and Mixture of Inputs). None of these approaches are suited for training with reinforcement learning approaches such as GRPO, which have become the leading post-training methods for improving reasoning performance.

In Soft Tokens, Hard Truths, the authors propose a simple and scalable method to implement continuous thoughts which integrates with RL training schemes. They use this to explore different configurations of “soft” continuous tokens and “hard” sampled tokens in both training and inference.

Figure 1. Hard, fuzzy and soft generation during CoT phase. In hard generation, at each time step, a discrete token $CoT_t$ is sampled from the probability vector $p_{t−1}$ and its embedding $h^0_{CoT1}$ is passed to the transformer, generating a sequence of discrete CoT tokens: $CoT_1, ..., CoT_T$ over time. In fuzzy and soft generation, at each time step, noise, $\epsilon_t$, is injected into the probability weighted mixture embedding, $h^t_0 = p_{t−1}E$, where E is the token embedding matrix. This noisy input embedding is passed to the transformer, generating a sequence of continuous noisy CoT embeddings: $\tilde{h}^0_{CoT_1}, ..., \tilde{h}^0_{CoT_T}$ over time. Additionally, for fuzzy generation, the temperature $\tau$ used in the CoT phase tends to $0$, such that the non-noisy embeddings $h_0$ reduce to embeddings of discrete tokens. We find that the combination of soft/fuzzy training and hard inference performs universally best, matching hard training at pass@1 and surpassing it at pass@$32$, indicating better preservation of diversity.

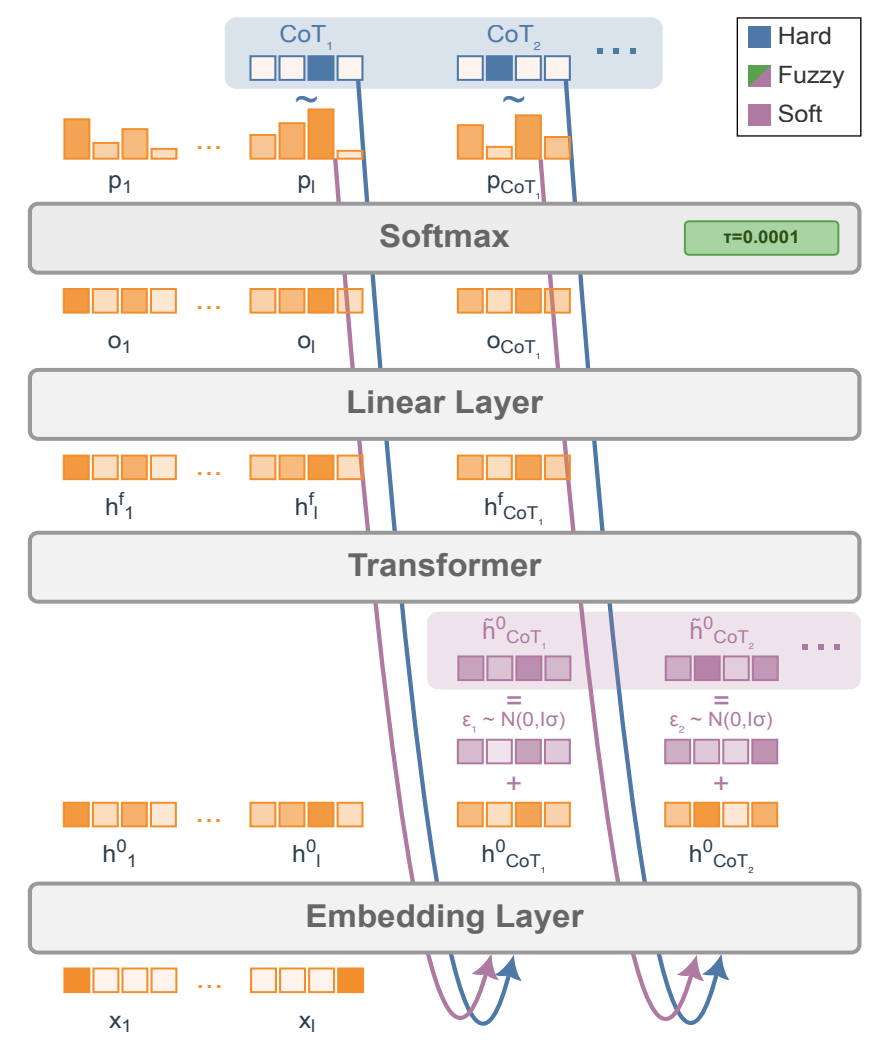
Their method

One approach to obtain continuous tokens from a pre-trained LLMs is by using the final softmax from the previous forward pass. Instead of sampling from the probability distribution to determine the next token (which is subsequently fed into the model as the input in the next forward pass), the probability distribution can be used as weights to make a probability-weighted average of the input embeddings to create a “soft token”. On the next forward pass, we can skip the initial embedding layer, and instead pass the soft token straight into the LLM. Works such as Soft Thinking have found that pre-trained models are fairly robust to this sort of interpolation, and are able to obtain good task performance without any additional training.

SOTA reinforcement learning approaches such as GRPO rely on generating several reasoning traces and answers, which are then used to determine advantages which provide the signal used for backpropagation. The challenge with soft tokens is that, because reasoning tokens are now no longer sampled (but rather deterministic interpolations of the input embedding space), there is no diversity across reasoning traces. This greatly limits the exploration that RL fine-tuning methods require. To address this, the authors propose injecting random noise on the input embeddings. This allows different rollouts to have different trajectories, greatly improving the exploration for RL to learn from.

Results

The authors considered chain-of-thought models with the following paradigms:

• For training:
  • Hard tokens: the conventional LLM generation approach in which tokens from the vocabulary are sampled.
  • Soft tokens: using the output probability distribution to weight the input embeddings (softmax temperature = $0.5$).
  • Fuzzy tokens: Similar to soft tokens, but with a softmax temperature $0.0001$, which makes them very close to hard tokens, before adding Gaussian noise.
• For inference:
  • Hard Greedy: discrete tokens, CoT temperature $\tau=0.0$ at test time
  • Hard Sample: discrete tokens, CoT temperature $\tau=1.0$ at test time
  • Soft Greedy: Gaussian scale $0.0$, CoT temperature $\tau=0.5$ at test time
  • Soft Sample: Gaussian scale $\sigma=0.33 *$ RMSNorm of embeddings, CoT temperature $\tau=0.5$ at test time
  • Fuzzy Greedy: Gaussian scale $0.0$, CoT temperature $\tau=0.0001$ at test time
  • Fuzzy Sample: Gaussian scale $\sigma=0.33 *$ RMSNorm of embeddings, CoT temperature $\tau=0.0001$ at test time

Base models include Llama 3.2 3B Instruct, Llama 3.1 8B Instruct, and Qwen 2.5 3B Instruct, trained on math reasoning datasets GSM8K, MATH and DeepScaleR. Test performance was evaluated on GSM8K, OlympiadBench, and the MATH-500 subset of the MATH test set.

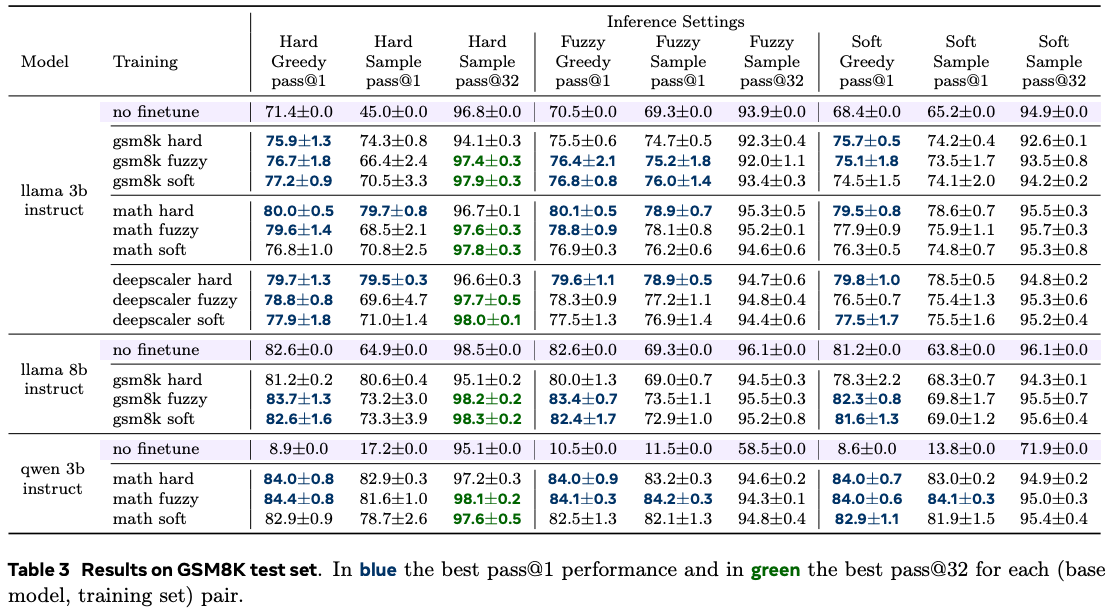
The results found that, across datasets and models, the three training schemes were broadly comparable with evaluating pass@$1$ performance. However, when considering pass@$32$ performance, soft and fuzzy training attain a superior performance. They also find that soft and fuzzy training is better when inferring on out-of-distribution data. For inference, the authors found that hard inference attains the best performance in general, regardless of the training scheme.

Conclusion

Soft Tokens, Hard Truths introduces a framework for using SOTA RL algorithms in a continuous thought paradigm. Their results demonstrate the benefits of continuous thoughts during training, however the observation that sampling during inference is better is a somewhat surprising result; we will be keenly watching this space as the community better understands this behaviour, and continues to advance the field of latent reasoning.