Speculative Streaming: Fast LLM Inference without Auxiliary Models
The key idea
Speculative decoding is great for speeding up LLM inference, but has the downside of requiring a well-aligned external draft model. Speculative streaming addresses this by modifying a model to produce its own tree of draft tokens in one parallel inference step.
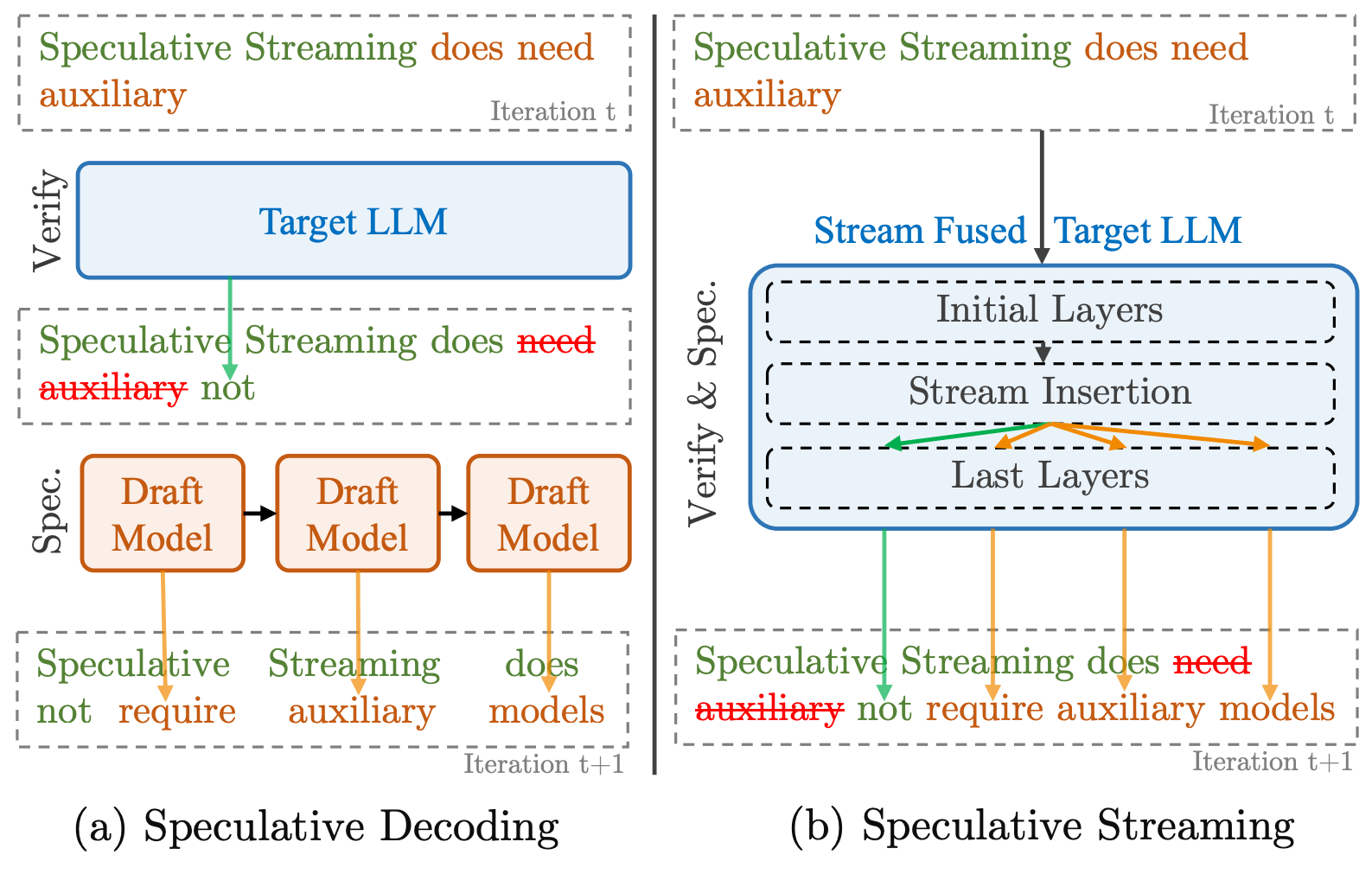
Background
Over the last year, speculative decoding (or speculative sampling) has become popular for LLM inference. This works by using a smaller draft model alongside the main target model, whose job it is to generate a sequence of draft tokens at each step. The target model then verifies those proposed tokens (checking to see if they are sufficiently aligned with its own probability model) and accepts them up to some point in the draft sequence. Accepted tokens become part of the “true” output of the model and rejected ones are disposed of.
This process has two crucial properties that make it appealing:
- The target model can verify draft tokens in parallel. This makes it more efficient than typical token-by-token generation.
- Due to some neat maths, the accept/reject process means that the distribution of the tokens is exactly that of the target model. I.e. there is no degradation when using speculative decoding!
However, off-the-shelf draft models can give quite different predictions to the target model so often need fine-tuning for alignment, and running two models simultaneously can be complex and memory-intensive.
Their method
The authors address this by adapting existing models and fine-tuning, such that the model can generate its own draft tokens.
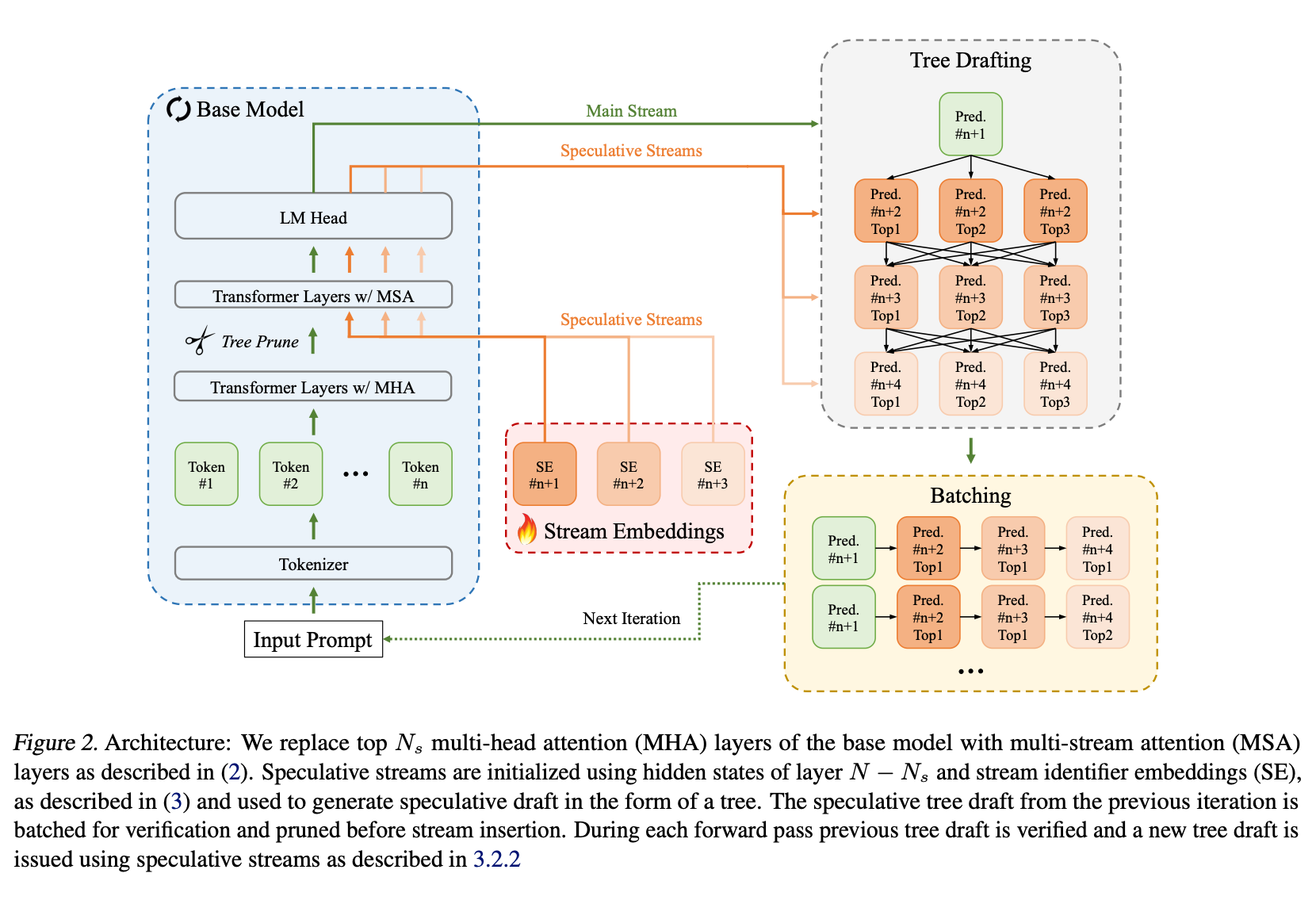
This is done via a process of parallel pruning, speculation and verification. This can be a little tricky to understand, as each inference step is now doing three things: verifying the previous draft tokens, generating a new token after the draft sequence, and generating the next draft tokens. It works as follows:
Each iteration takes as input the sequence so far, along with a (flattened) tree of draft tokens. A special pruning layer in the middle of the network uses the final embedding layer to generate an early prediction of which trees look promising, dropping low-probability branches. This is followed by a stream embedding layer, which uses the regular tokens’ hidden state to generate a set of hidden states for a tree of “new” draft tokens.
These new draft tokens are processed in the usual way until the end of the network, where the model uses the standard speculative decoding accept/reject sampling to decide which “input” draft tokens to accept. The “new” draft tokens generated for that branch then become the “input” draft tokens for the next iteration.
Results
Speculative streaming is substantially faster than regular auto-regressive inference, and is marginally faster than the competing Medusa method (which also adapts a single model to produce a draft) but uses many fewer additional parameters.
The comparison against standard speculative decoding is harder. Their empirical results show a 2x speedup, but depend on various practical considerations and hyperparameters. More useful is their theoretical analysis showing the regimes in which speculative streaming should give a speedup. There are clearly circumstances in which it’s beneficial, though this heavily depends on the relative quality of the draft models:
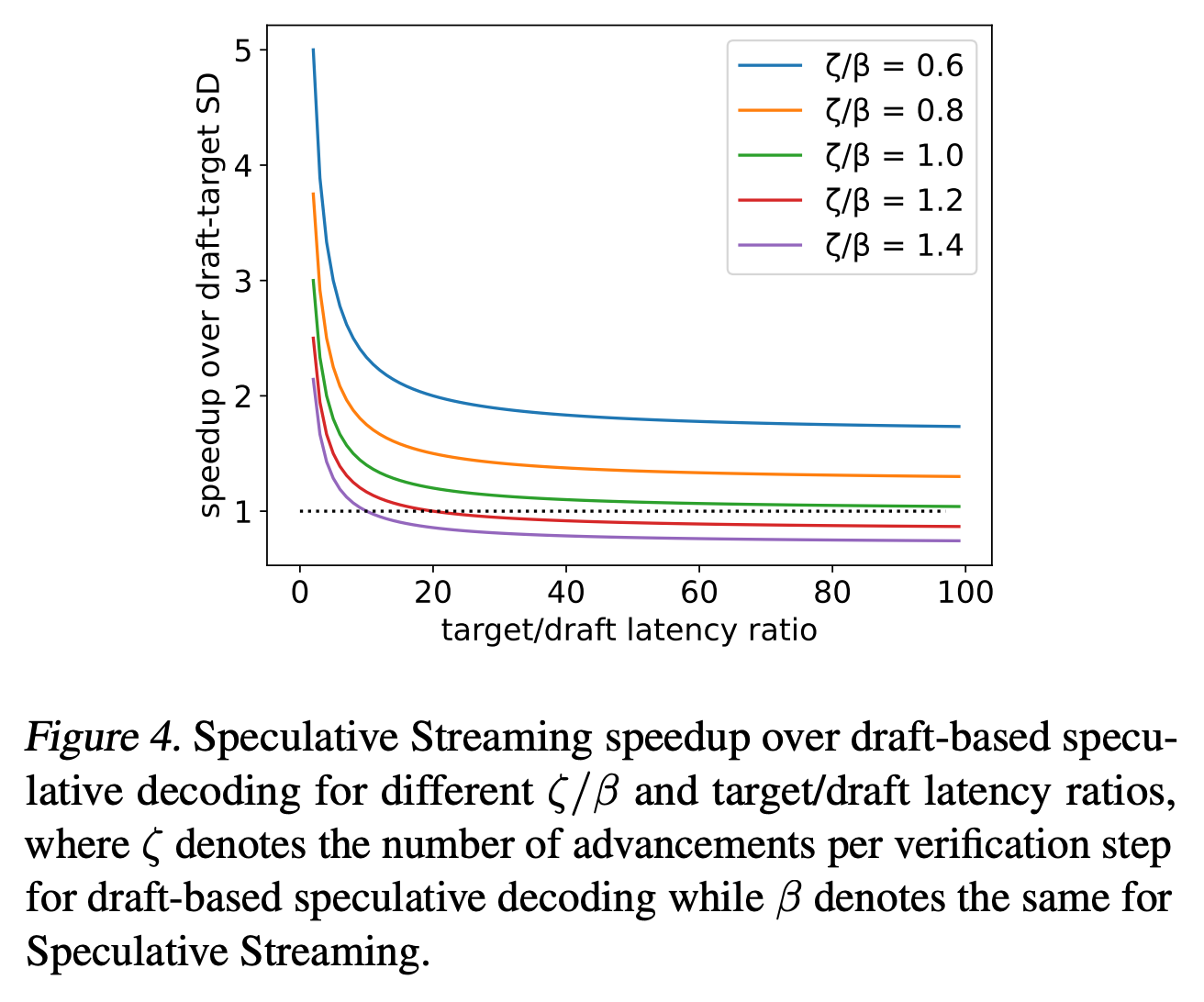
Takeaways
This is a really neat paper, even if it feels like a bit of a “hack” in the context of auto-regressive LLMs. Predicting multiple tokens in parallel is not really something that LLMs should excel at, and they only get away with it here because of the speculative setting. But because it allows a single model to do both draft and target modeling in a single step, it appears to be worthwhile.
Given all that, their execution of the idea is great. The authors are clearly concerned with making this work in practical settings, which is reflected by their addition of tricks like tree pruning. The results look promising, though it remains to be seen which areas of their speedup-modeling correspond to practical use-cases, which will ultimately determine how widely speculative streaming is used.





Comments