Scaling Laws with Vocabulary: Larger Models Deserve Larger Vocabularies

The key idea

Scaling laws (e.g. Kaplan, Chinchilla) have proved enormously useful in showing how to most efficiently scale LLMs for a given FLOPs budget but these scaling laws have generally only considered non-vocabulary parameters. This paper attempts to address that issue by calculating scaling laws for the vocabulary parameters and finds that many public LLMs are underparameterised for vocabulary. The authors use three complementary approaches to fit a power law: IsoFLOPs analysis, derivative estimation and parametric fit of the loss function. They show empirically that vocabulary parameters should be scaled with model size but at a slower rate than non-vocabulary parameters.

Their method

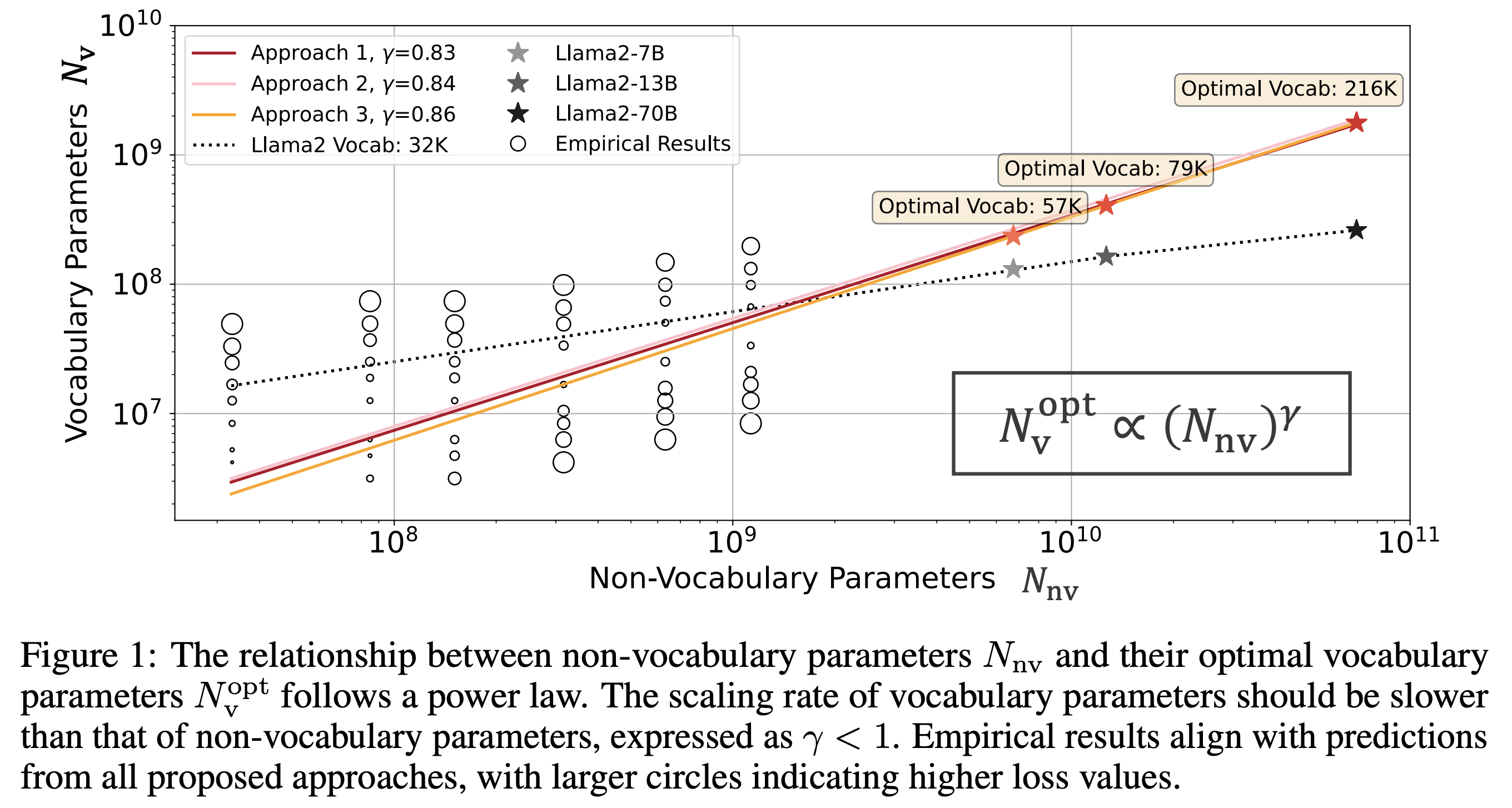
The authors use three complementary approaches in the paper. Firstly they use an IsoFLOP analysis wherein a series of models with varying vocabulary parameters were trained with fixed FLOPs and fixed non-vocab parameters. Observing the vocab size at minimum loss for each FLOP budget allowed them to fit power laws for vocab size and non-vocab parameters.

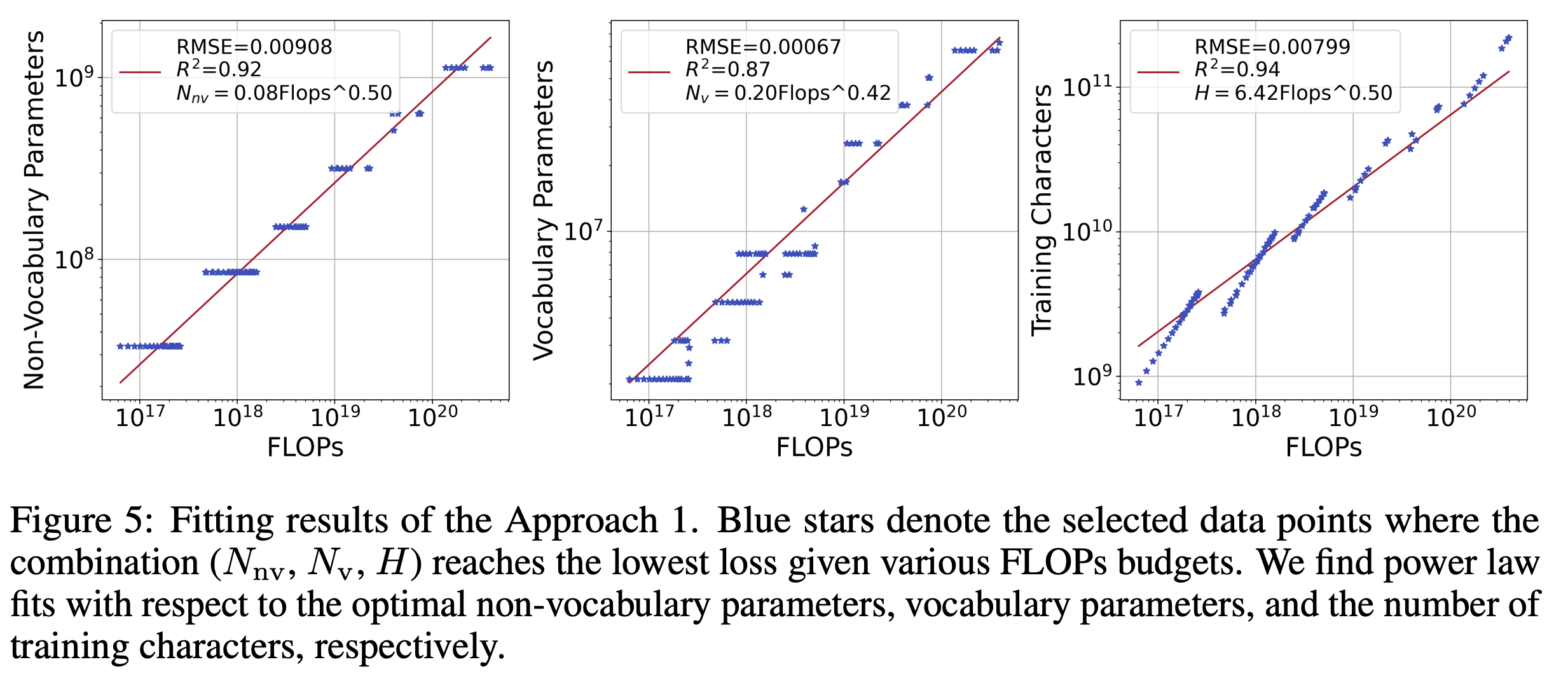
The second approach uses a derivative based method wherein a formula is derived for flops based on a derived formula for FLOPs based on both vocabulary and non-vocabulary parameters as well as training tokens. Then by finding the minimum of this function with respect to vocabulary (V), they can estimate the optimal V under the assumption that it can achieve a certain loss. This feels like quite a strong assumption nonetheless the results match closely with those from approaches 1 and 3.

Finally, a third approach uses a parametric vocabulary dependent loss formula:

$ L_u = -E + \frac{A_1}{N_{nv}^{\alpha_{1}}}+\frac{A_2}{N_{v}^{\alpha_{2}}}+\frac{B}{D^{\beta}} $

The first term captures the normalised loss for an ideal generative process and the subsequent terms respectively reflect the effect of non-vocab parameters, vocab parameters and the amount of training data on the loss. Using the experiments from the IsoFLOP analysis the authors can learn the optimal parameters for the loss formula and subsequently predict the optimal vocabulary configuration by finding the minimum point of the loss with respect to the vocabulary.

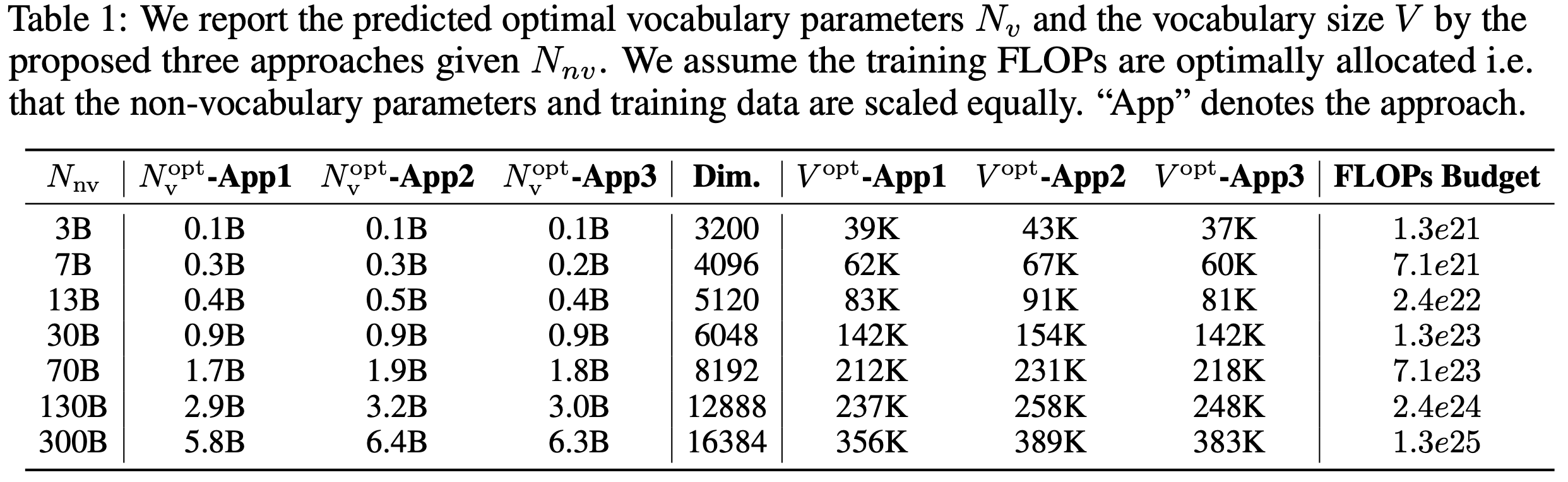
The authors find that all three approaches agree closely in that non-vocab parameters should be scaled faster than vocabulary parameters.

Results

The authors show their predictions in action by training 3B parameter models with their standard 32K vocab size and comparing this with their predicted optimal vocab size of 35K. They show that this leads to improvements on various benchmarks with only a small adjustment to vocab size.

The overall takeaway is that according to their analysis, most public LLMs are underparameterised for their vocabulary and that when scaling up model size, vocab size ought to be increased too but at a slower rate than the other parameters.